Глава IV. Векторы в пространстве Дополнительные задачи → номер 388
Чтобы доказать компланарность, достаточно показать, что один вектор раскладывается по двум другим векторам. а) Пусть
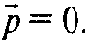
Тогда
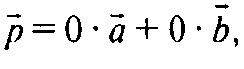
Что и означает, что векторы
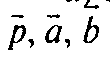
Компланарны. б) Пусть
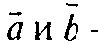
— коллинеарны, т. е.
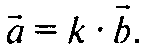
Тогда
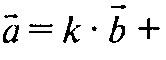
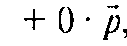
Т. е.
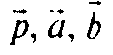
Компланарны.
