Глава V. Метод координат в пространстве. § 3. Движения → номер 484 484. Докажите, что при параллельном переносе на вектор р, где р≠0: а) прямая, не параллельная вектору р и не содержащая этот вектор, отображается на параллельную ей прямую; б) прямая, параллельная вектору р или содержащая этот вектор, отображается на себя.
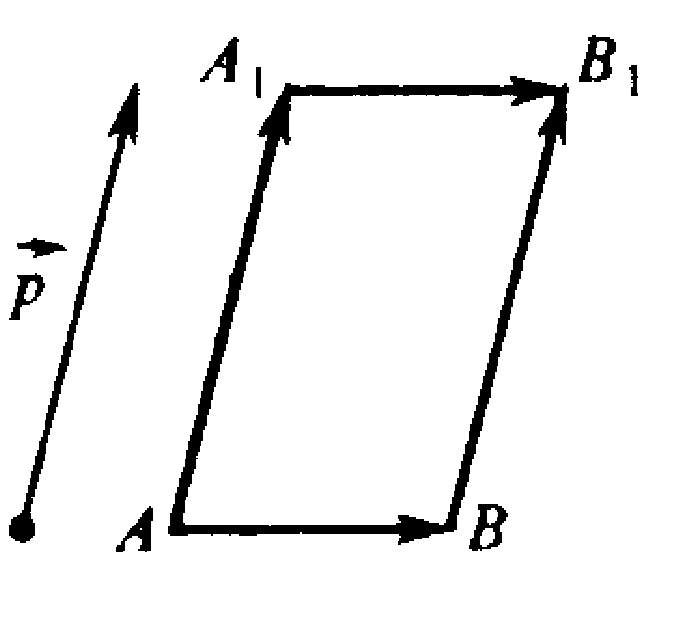
а) Докажем, что АВ||А1В1 (см. пункт 52 учебника). Доказано, что А1В1=АВ, а значит А1В1||AB.
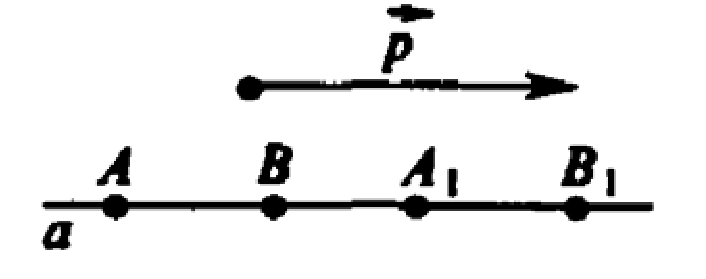
Б) Пусть а || p. Выберем точку А ∈ а, тогда точка А перейдет в точку А1, так, что АА1= p. Следовательно, они лежат в одной плоскости. В плоскости через точку А можно провести только одну прямую АА1, параллельную p, тогда А1∈ а.
Таким образом, точка А ∈ а отображается в точку А1 ∈ а.
Для любой другой точки В ∈ а повторим рассуждения, тогда, каждая точка прямой а переходит в точку прямой а, то есть прямая отображается на себя.
Пусть а содержит p, тогда доказательство верно, просто векторы АА1 и
P лежат на одной прямой а.