Глава V. Метод координат в пространстве. § 3. Движения → номер 488
а) Пусть а || b, а ⊂ α, b ⊂ α. Пересечем а и b прямой с, следовательно ∠1=∠2 как внутренние накрест лежащие при параллельных а, b и секущей с. Примем следующие обозначения (смотри рисунок):
М и N — произвольные точки, лежащие по разные стороны от секущей АВ.
При движении ∠МAB перейдет в равный ∠М1A1B1, a ∠ABN — в равный угол ∠A1B1N1. Т. к. при движении плоскость α переводится в плоскость β, то прямые A1M1 и B1N1 лежат в одной плоскости β.
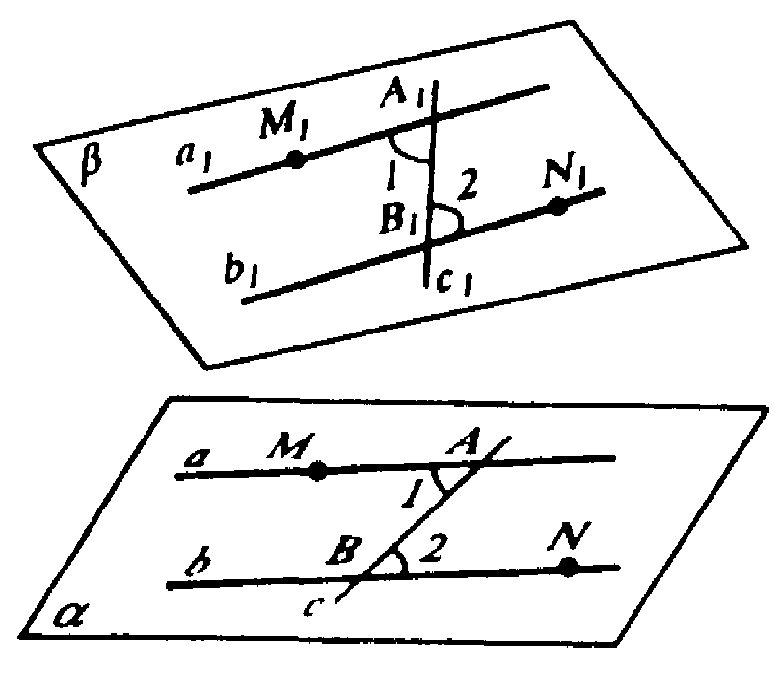
Отмеченные углы — ∠1 и ∠2, являются внутренними накрест лежащими, а если ∠1=∠2, то по признаку параллельности прямых М1A1 || B1N1, или а1 || b1. тогда, а → а1, а || а1 и b → b1, b || b1.
Б) α || β. Пересечем α и β плоскостью С, получим две параллельные прямые A1B1 || АВ.
На линии пересечения плоскости С с плоскостью β через некоторую точку А1 проведем плоскость Q, пересекающую α и β по параллельным прямым А1С1 и АС.
Построим отрезки B1С1 и ВС. Отрезки параллельных прямых, заключенные между параллельными плоскостями равны, тогда АА1=ВВ1=СС1.
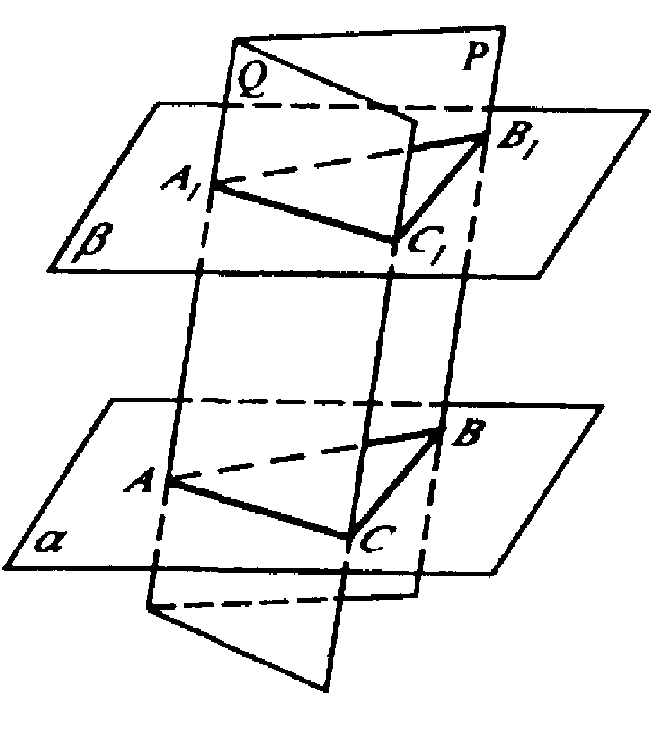
АВСА1B1С1 — призма. При движении угол отображается на равный ему угол, расстояния между точками сохраняются. При этом, очевидно, основания призмы — ΔA1B1C1 и ΔАВС остаются параллельными друг другу, и плоскости, которые можно провести через вершины A, В, С и A1, B1, C1, будут также параллельны друг другу.
