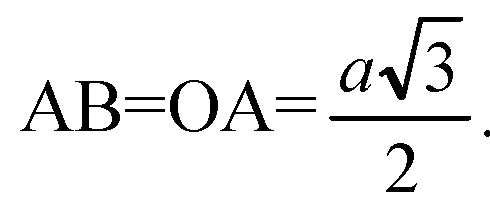Глава VI. Цилиндр, конус и шар § 3. Сфера → номер 591
Построим сечение плоскостью, проходящей через центр шара, (точку О), и перпендикулярной ребру двугранного угла MN. Тогда построенная плоскость перпендикулярна α и β. Проведем ОВ перпендикулярно к плоскости α и ОА перпендикулярно к плоскости β. OB = OA = R.
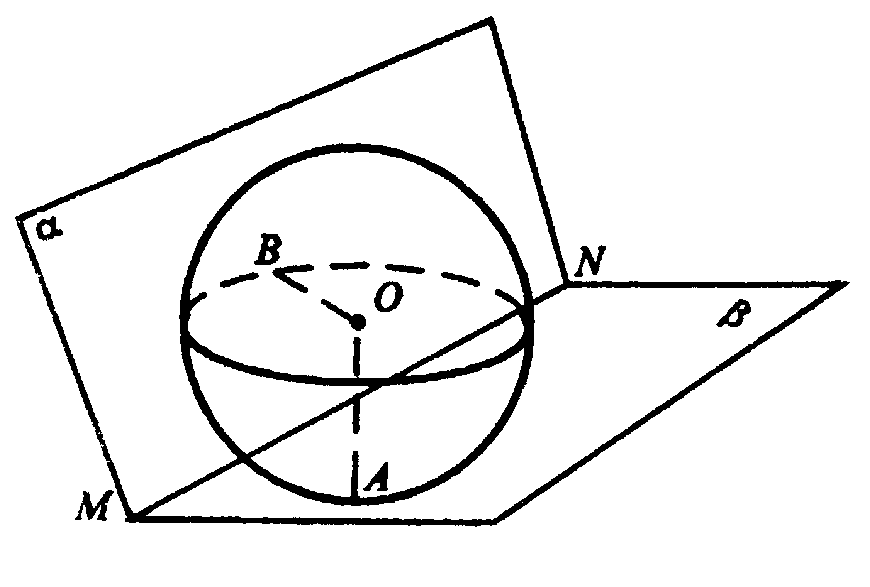
ОА ⊥ β, АС ⊥ MN (по построению).
ОС⊥МN — по теореме о трех перпендикулярах.
ОС — расстояние от центра сферы до ребра MN, ОС=а. ΔОВС=ΔОАС (ОВ=ОА=R, ОС — общая), тогда ОС — биссектриса угла ∠АСВ, ∠АСВ=120o,
Тогда, ∠ОСА= 60 °. Из ΔОСА имеем:
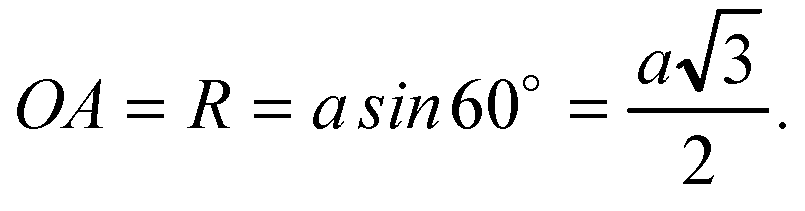
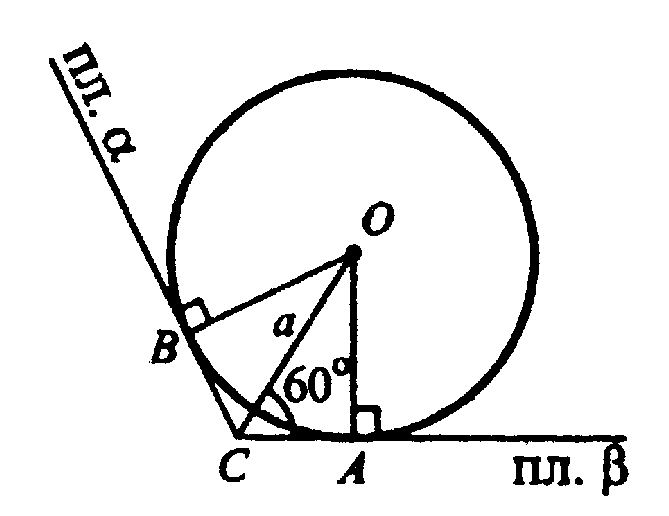
AB — расстояние между точками касания.
ΔАОВ — равнобедренный, ∠ОСА=60o, тогда,
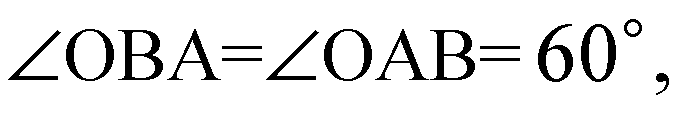
ΔАОВ — равносторонний,