75. Изобразите тетраэдр KLMN. а) Постройте сечение этого тетраэдра плоскостью, проходящей через ребро KL и середину А ребра MN. б) Докажите, что плоскость, проходящая через середины Е, О и F отрезков LM, МА и МК, параллельна плоскости LKA. Найдите площадь

Глава I Параллельность прямых и плоскостей. §4 Тетраэдр и параллелепипед. → номер 75 75. Изобразите тетраэдр KLMN. а) Постройте сечение этого тетраэдра плоскостью, проходящей через ребро KL и середину А ребра MN. б) Докажите, что плоскость, проходящая через середины Е, О и F отрезков LM, МА и МК, параллельна плоскости LKA. Найдите площадь треугольника EOF, если площадь треугольника LKA равна 24 см2.

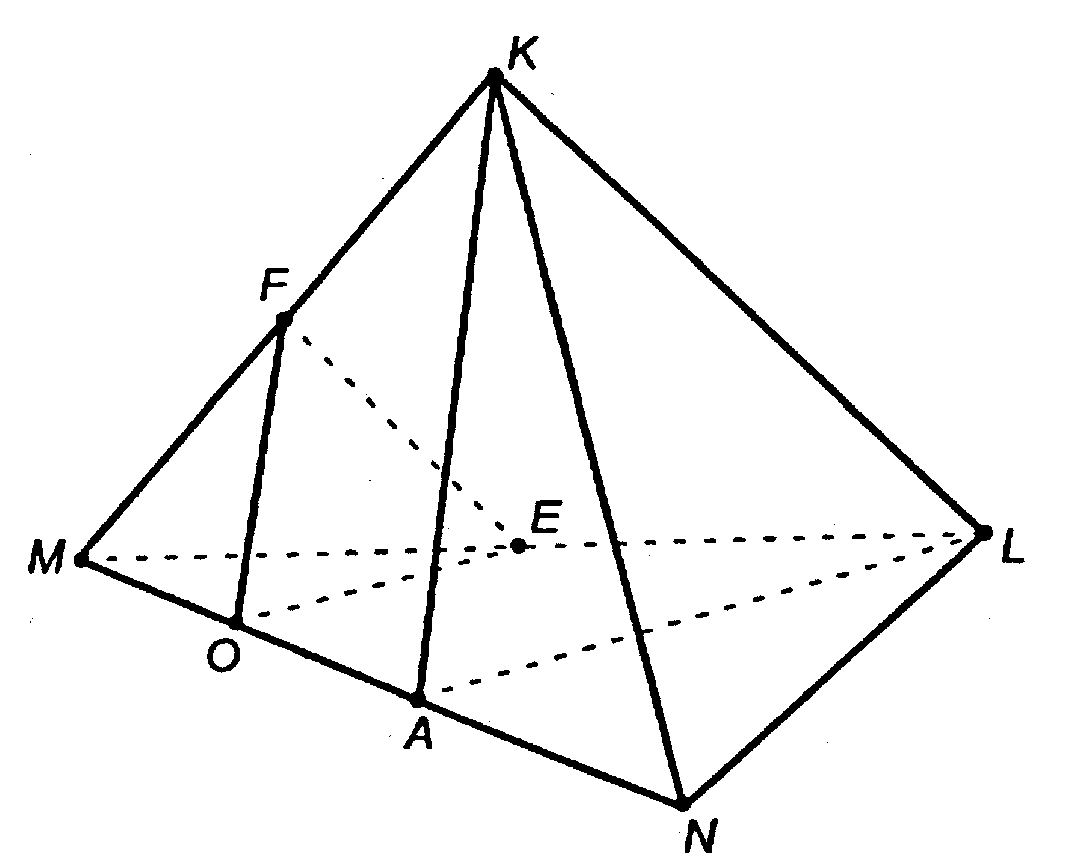
А) Проведем

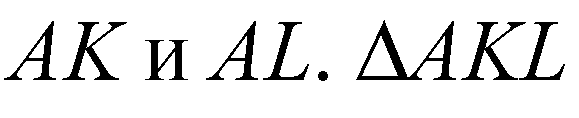
— искомое сечение.

Б) В ΔAMK: OF — средняя линия, OF || AK; в ΔMLK: EF — средняя линия, EF || KL.

По теореме п. 10

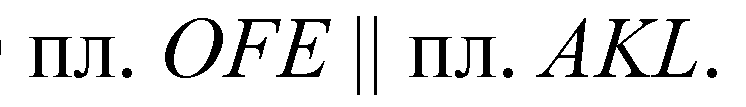
Площади подобных треугольников

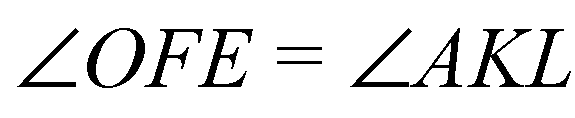
Как углы с соответственно параллельными и одинаково направленными сторонами;

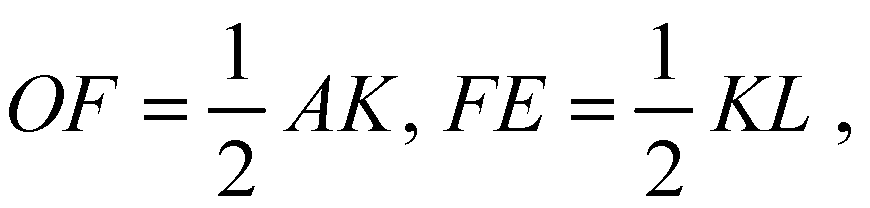
Поэтому

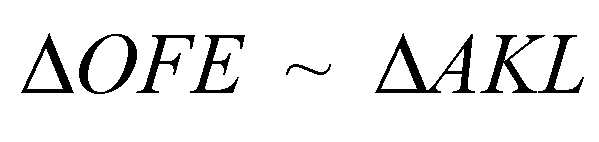
Относятся как квадраты, значит, соответствующих линейных размеров.