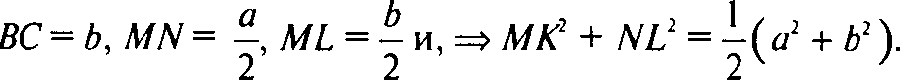766. Докажите, что сумма квадратов двух противоположных ребер тетраэдра вдвое больше суммы квадратов отрезков, соединяющих соответственно середины остальных противоположных ребер

Задачи повышенной трудности → номер 766

В обозначениях рисунка к задаче 765 по свойству средней линии MN || AD || LK, аналогично ML || NK и MNKL — параллелограмм.

Тогда

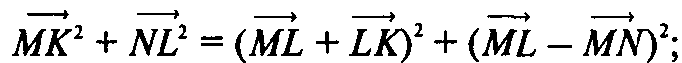
Т. к.

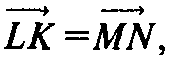
То

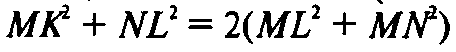
— сумма квадратов диагоналей па-

Раллелограмма равна сумме квадратов всех его сторон. Если

И