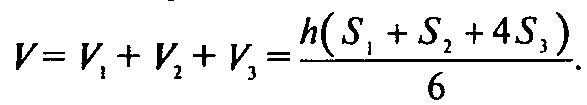Задачи повышенной трудности → номер 808
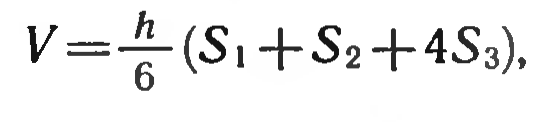 где V — объем многогранника, h — его высота, S1 и S2 — площади оснований, а S3 — площадь сечения плоскостью, параллельной плоскостям оснований и равноудаленной от них.
где V — объем многогранника, h — его высота, S1 и S2 — площади оснований, а S3 — площадь сечения плоскостью, параллельной плоскостям оснований и равноудаленной от них.
Пусть О — какая-нибудь точка на среднем сечении данного многогранника. Разобьем его на пирамиды с вершиной О. Основаниями двух из них будут служить основания многогранника, основаниями остальных — треугольники, из которых состоят его боковые грани. Объемы первых двух пирамид:
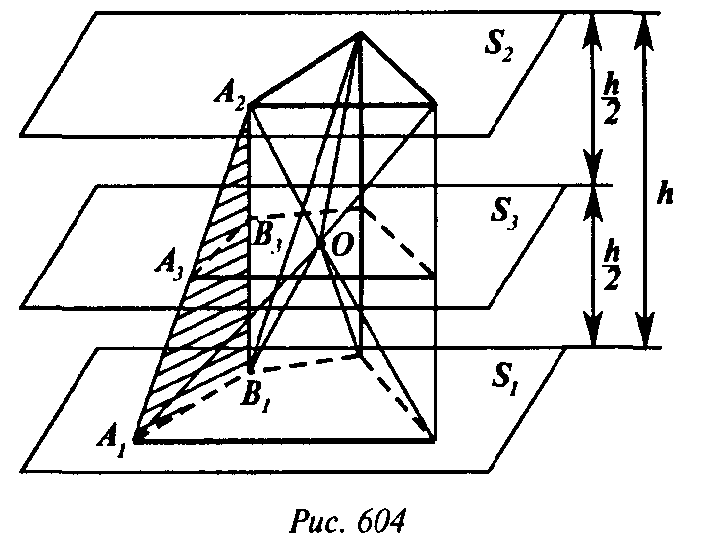
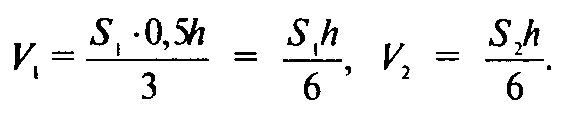
Если ΔA1B1A2 — один из
Треугольников, на которые разбиты боковые грани, то среднее сечение пересечет его по средней линии A3B3 Тогда
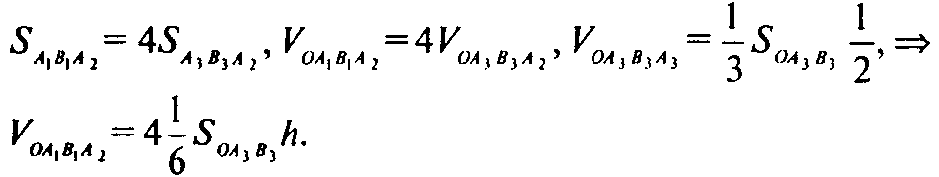
Так как сумма площадей всех таких треугольников равна S3, то сумма объемов всех пирамид с основаниями на боковых гранях
Равна
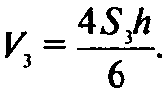
Объем всего многогранника равен