Дано:
Через неподвижный блок перекинута нить, к одному концу которой прикреплен груз m1, а к другому — второй блок. Через второй блок также перекинута нить с грузами m2 и m3 на концах. Ускорения грузов равны соответственно a1, a2 и a3. Массами блоков и трением в них можно пренебречь. Ускорения считаются положительными, если они направлены вниз. m1=7,2 кг, a2=+0,9 м/(с*c), a3=-4,1 м/(с*c), m3-?
Решение
Изобразим всю систему на схеме (рис.1).
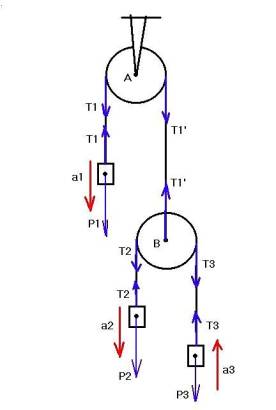
Рассмотрим сначала движение внутри подсистемы грузов 2 и 3. Для этого начало СК свяжем с точкой B. В этой СК:
m2*a2’=P2-T2 (1)
m3*a3’=P3-T3 (2)
Так как нить B нерастяжима, то a3’= -a2’ (3a). А поскольку она невесома, то T2-T3=0 => T2=T3 (3b). Кроме того, P2=m2*g, P3=m3*g (3c)
Подставляя (3) в (1-2) и складывая, получим:
a2’*(m2-m3)=(m2+m3)*g-2*T2 =>
2*T2=(m2+m3)*g-a2’*(m2-m3) (4)
Поскольку блок В невесом, то при любом его ускорении:
T2+T3-T1’=0 => T1’= T2+T3=2*T2 (5)
Теперь можно рассмотреть движение груза 1:
m1*a1=P1-T1 (6)
Поскольку нить А невесома, то T1-T1’=0 => T1=T1’ (7a)
А поскольку она нерастяжима, то a1’=-a1 (7b)
(где a1’ — ускорение блока В). Кроме того, P1=m1*g (7c)
Подставляя (7) в (6) и учитывая (5), вместе с (1-2) получаем систему из 3-х уравнений с 5-ью неизвестными: a1, a2’, T1, m2 и m3. Чтобы сделать её разрешимой, остается добавить соотношения для ускорений груза 2 и 3 относительно точки А:
a2=a1’+a2’; a3=a1’+a3’
Которые с учетом (3) и (7) превращаются в
a2=-a1+a2’; a3=-a1-a2’ (8)
