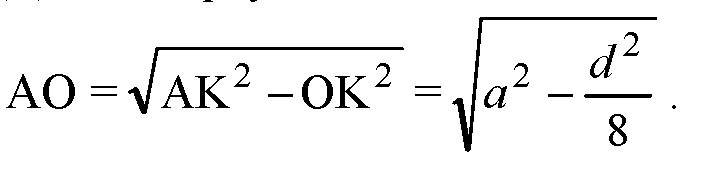§17. Перпендикулярность прямых и плоскостей → номер 50
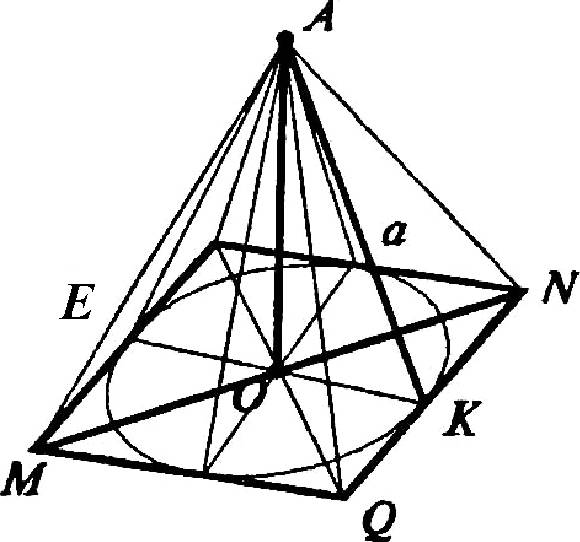
Пусть А — данная точка. АО — искомое расстояние, то есть AO — перпендикуляр. Наклонные АК = АЕ; ОЕ, ОК — проекции равных наклонных, а значит, ОЕ = ОК.
Далее по теореме о трех перпендикулярах ОЕ и ОК — перпендикулярны к сторонам квадрата. Значит, О — центр вписанной окружности. То есть О — точка пересечения диагоналей.
Тогда, ON = d/2 (по свойству диагоналей квадрата), и по теореме Пифагора в треугольнике OKN:
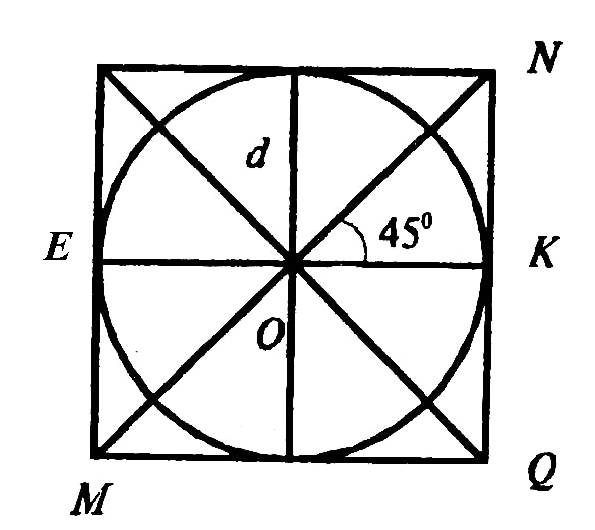
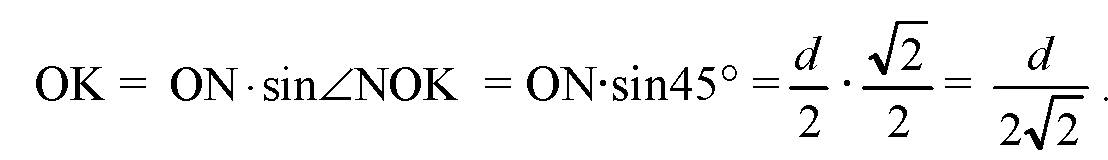
Далее в треугольнике АОК по теореме Пифагора: