Глава II Перпендикулярность прямых и плоскостей. §3 Двугранный угол. Перпендикулярность плоскостей. → номер 182
* В задачах этого параграфа двугранный угол с ребром АВ, на разных гранях которого отмечены точки С и D, для краткости будем называть так: двугранный угол CABD.
182. Плоскости α и β взаимно перпендикулярны и пересекаются по прямой а. Из точки М проведены перпендикуляры MA и MB к этим плоскостям. Прямая а пересекает плоскость АМВ в точке С. а) Докажите, что четырехугольник АСВМ является прямоугольником, б) Найдите расстояние от точки М до прямой а, если АМ = m, ВМ = n.
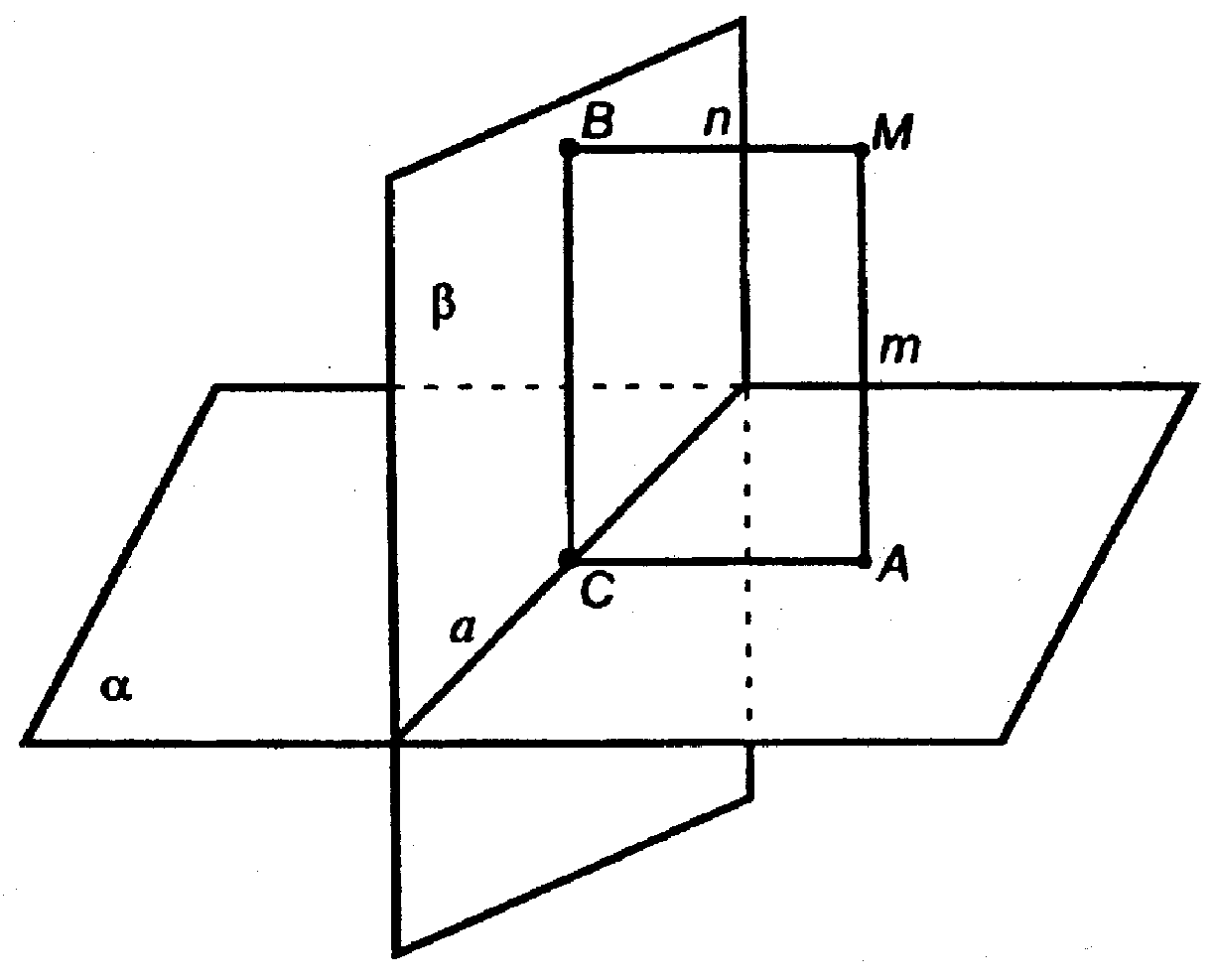
Дано:
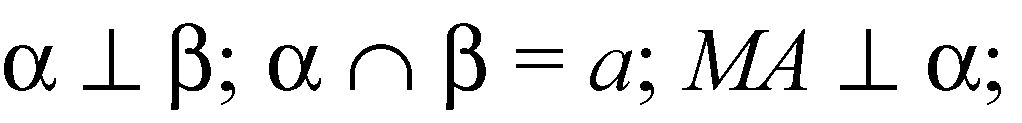
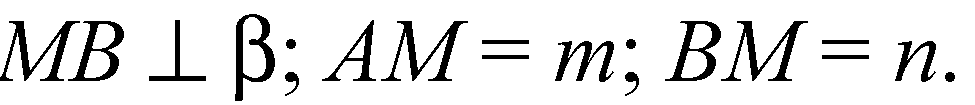
Решение:
В а проведем АС || MB; в β проведем отрезок ВС.
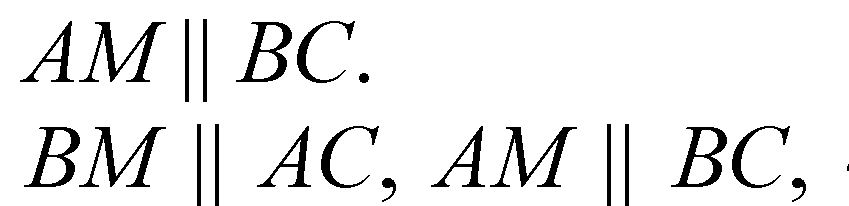
4-угольник
АСВМ — параллелограмм.
Раз
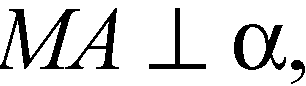
То
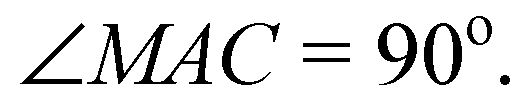
АСВМ — прямоугольник.
Раз
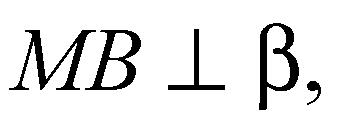
То
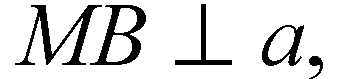
И поскольку
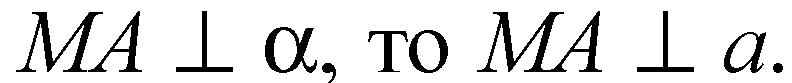
Отсюда
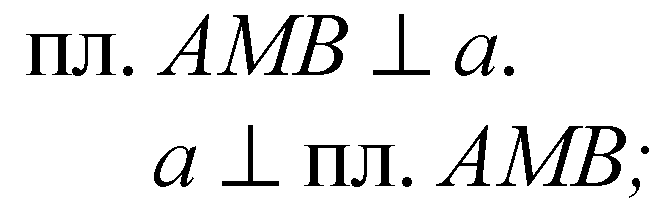
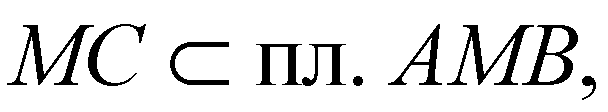
Отсюда
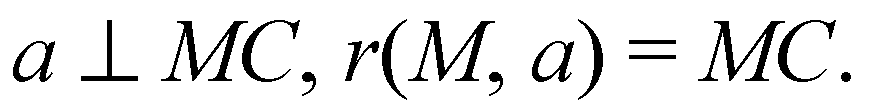
По теореме Пифагора:
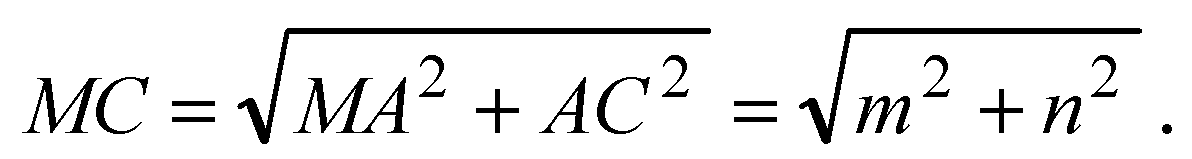
Ответ: