Глава II Перпендикулярность прямых и плоскостей. §3 Двугранный угол. Перпендикулярность плоскостей. → номер 183
* В задачах этого параграфа двугранный угол с ребром АВ, на разных гранях которого отмечены точки С и D, для краткости будем называть так: двугранный угол CABD.
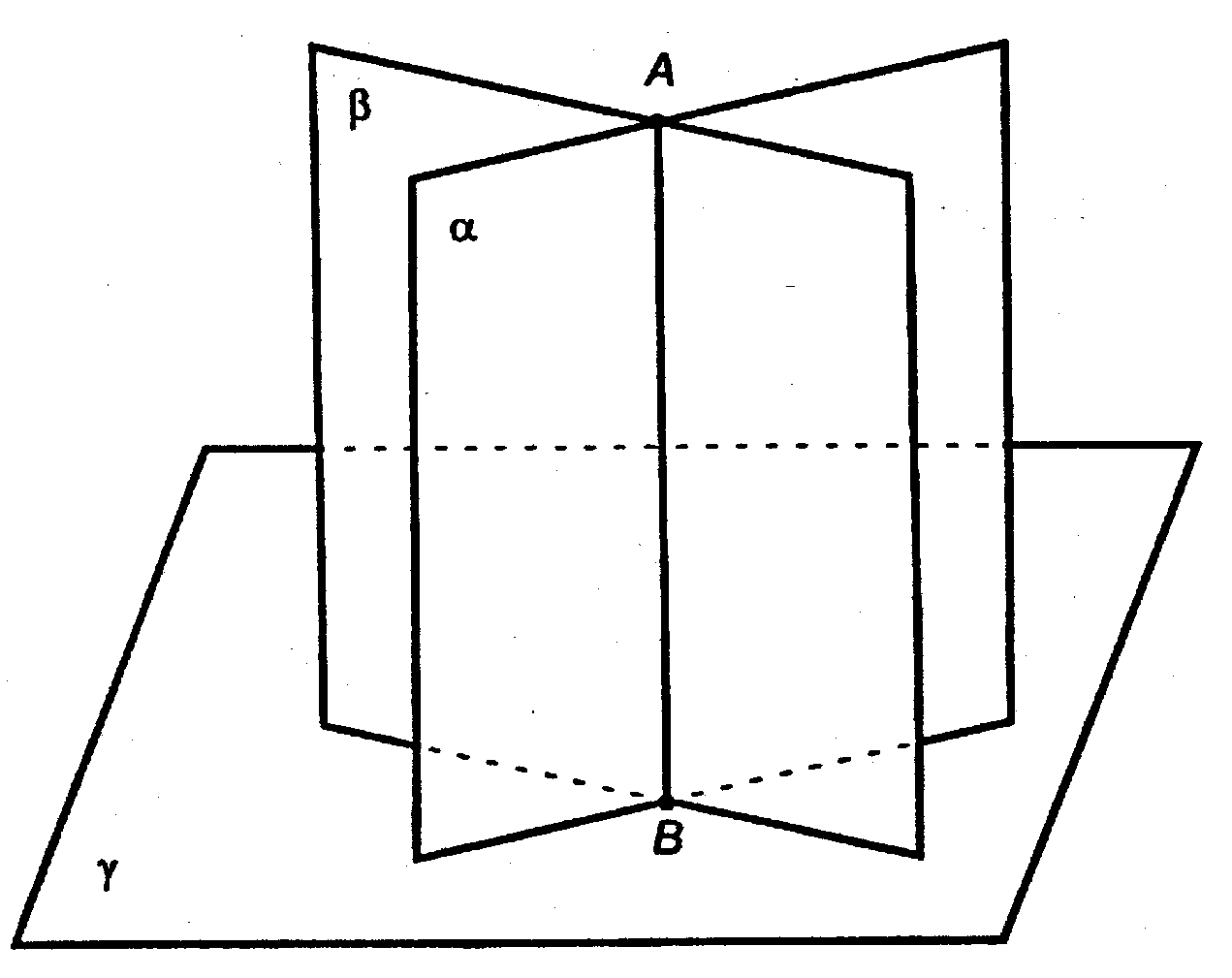
Дано:
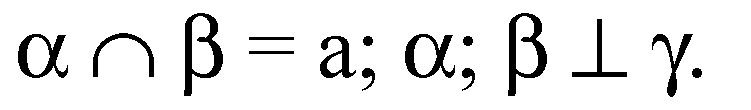
Решение:
Докажем следующее:
Если две плоскости (α и β) взаимно перпендикулярны и к одной из них (к β) проведен перпендикуляр (АВ), имеющий общую т. (А) с другой плоскостью (α), то этот перпендикуляр весь лежит в этой плоскости (а).
Это утверждение доказано в задаче 179.
Выберем произвольную т. А на линии пересечения а и в.
Проведем перпендикуляр к пл. γ.
По доказанному выше, этот перпендикуляр должен принадлежать и пл. а и пл. в, то есть
Он сливается с линией пересечения плоскостей, то есть с АВ. Утверждение доказано.
