Глава III Многогранники. §1 Понятие многогранника. Призма. → номер 224 224. Диагональ правильной четырехугольной призмы наклонена к плоскости основания под углом 60°. Найдите площадь сечения, проходящего через сторону нижнего основания и противолежащую сторону верхнего основания, если диагональ основания равна 4 √2 см.
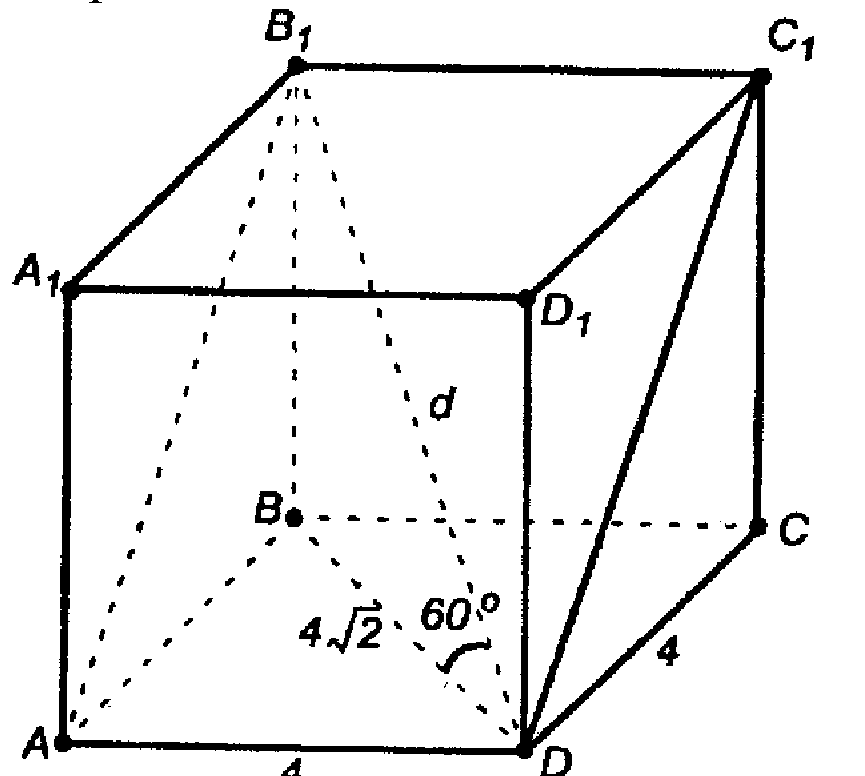
Решение:
AB1C1D — прямоугольник (АВ ⊥ AD, В1В ⊥ AD, по теореме о 3-х перпендикулярах АВ1 ⊥ AD, В1С1 || AD, значит, АВ1 ⊥ В1С1).
Пусть диагональ призмы B1D = d.
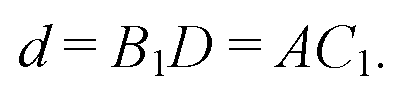
Из квадрата ABCD:
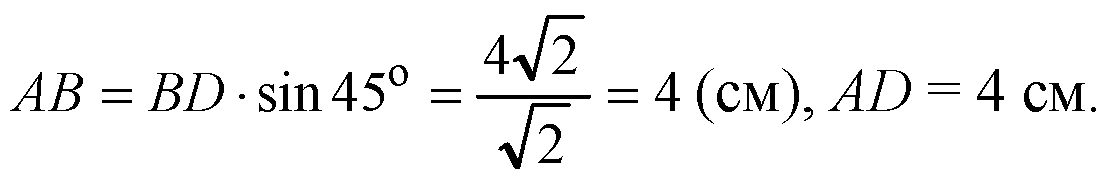
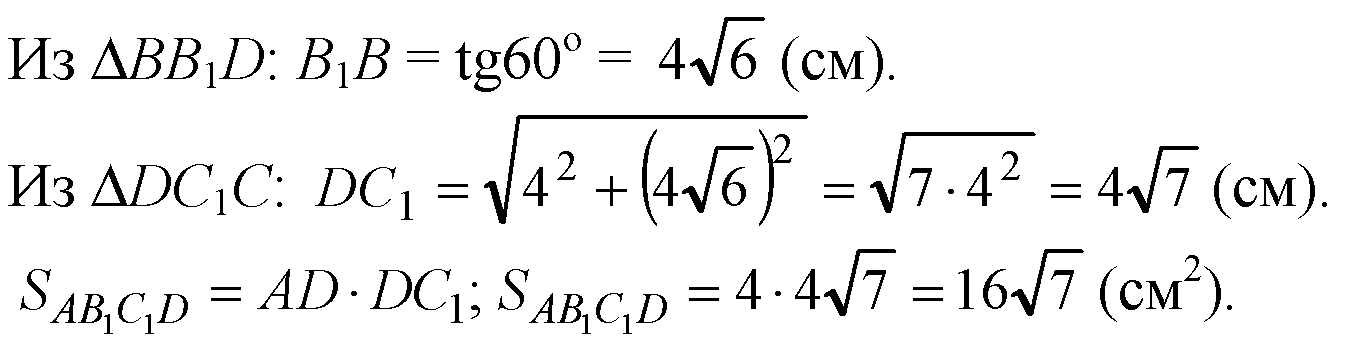
Ответ: 16√7 см2.
