227. Основание призмы — правильный треугольник ABC. Боковое ребро АА1 образует равные углы со сторонами основания АС и АВ. Докажите, что: а) ВС⊥АА1; б) СС1В1В — прямоугольник

Глава III Многогранники. §1 Понятие многогранника. Призма. → номер 227

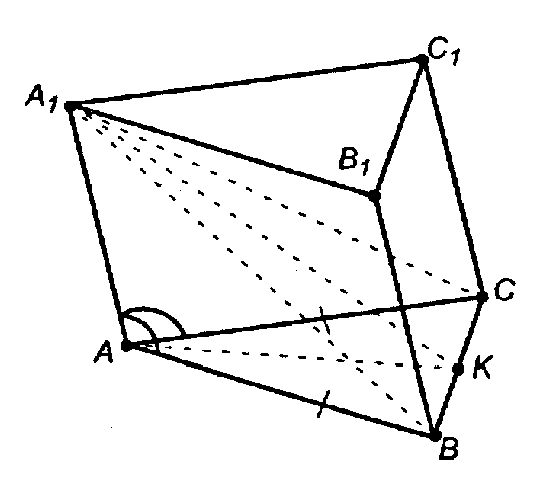
Решение:

В пл. АВС проводим медиану AK, AK ⊥ BC. Проведем отрезки А1В, А1С, A1K.

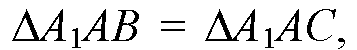
Так как А1А — общая, АВ = АС — по условию,

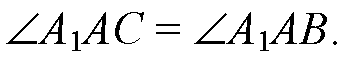
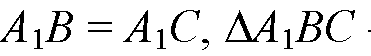
— равнобедренный, в нем отрезок А1K — медиана, поэтому

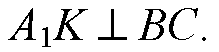
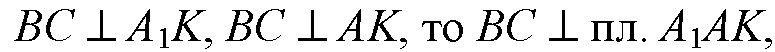
Поэтому

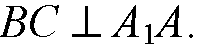
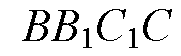
— параллелограмм,

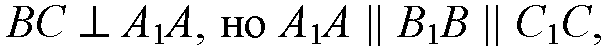
Значит,

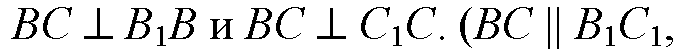
Поэтому

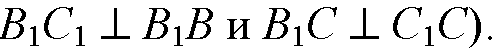
Параллелограмм, у которого хотя бы один угол прямой, есть прямоугольник, поэтому ВВ1С1С — прямоугольник.

Что и требовалось доказать.