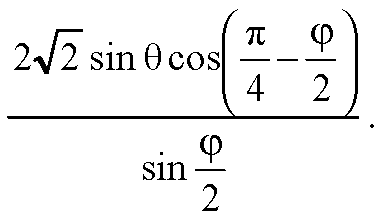Глава III Многогранники. §1 Понятие многогранника. Призма. → номер 235 235. Основанием прямой призмы является прямоугольный треугольник с острым углом φ. Через катет, противолежащий этому углу, и через противоположную этому катету вершину основания проведено сечение, составляющее угол Θ с плоскостью основания. Найдите отношение площади боковой поверхности призмы к площади сечения.
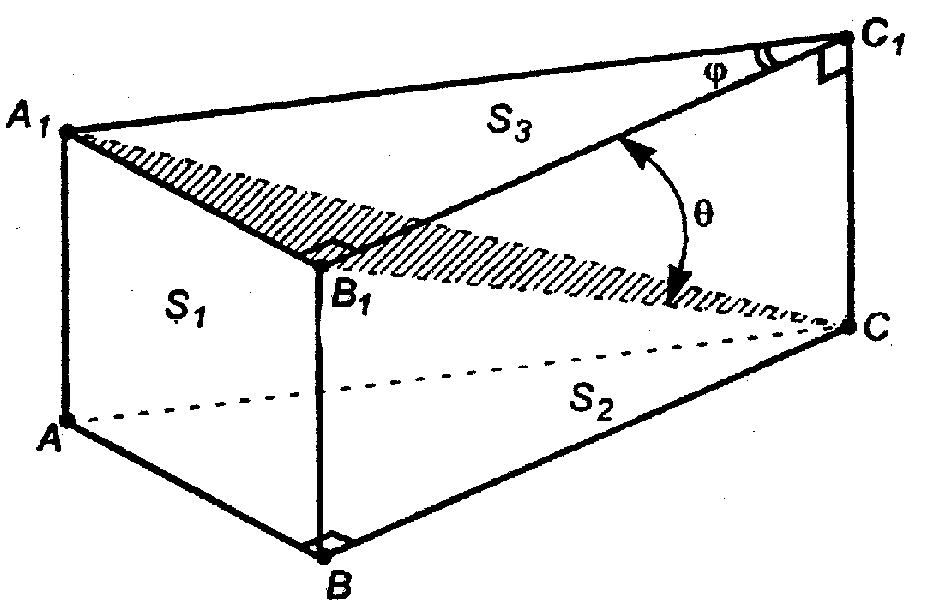
Решение:
Сечение — это ΔА1В1С. Отыщем линейный угол двугранного угла С1А1В1В.
С1В1 ⊥ В1А1, СВ1 ⊥ В1А1, то РС1В1С есть линейный угол данного двугранного угла.
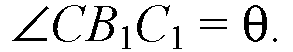
Пусть
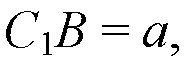
Тогда
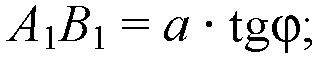
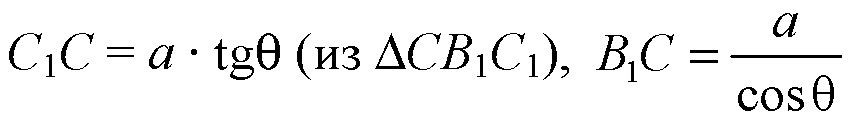
ΔА1В1С — прямоугольный,
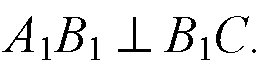
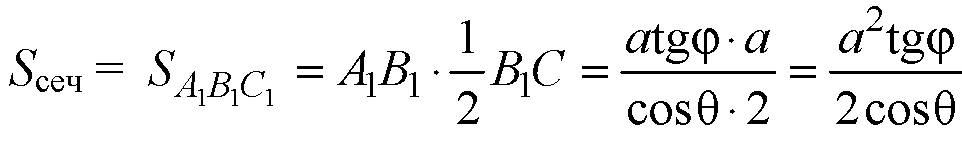
Все боковые грани являются прямоугольниками, значит,
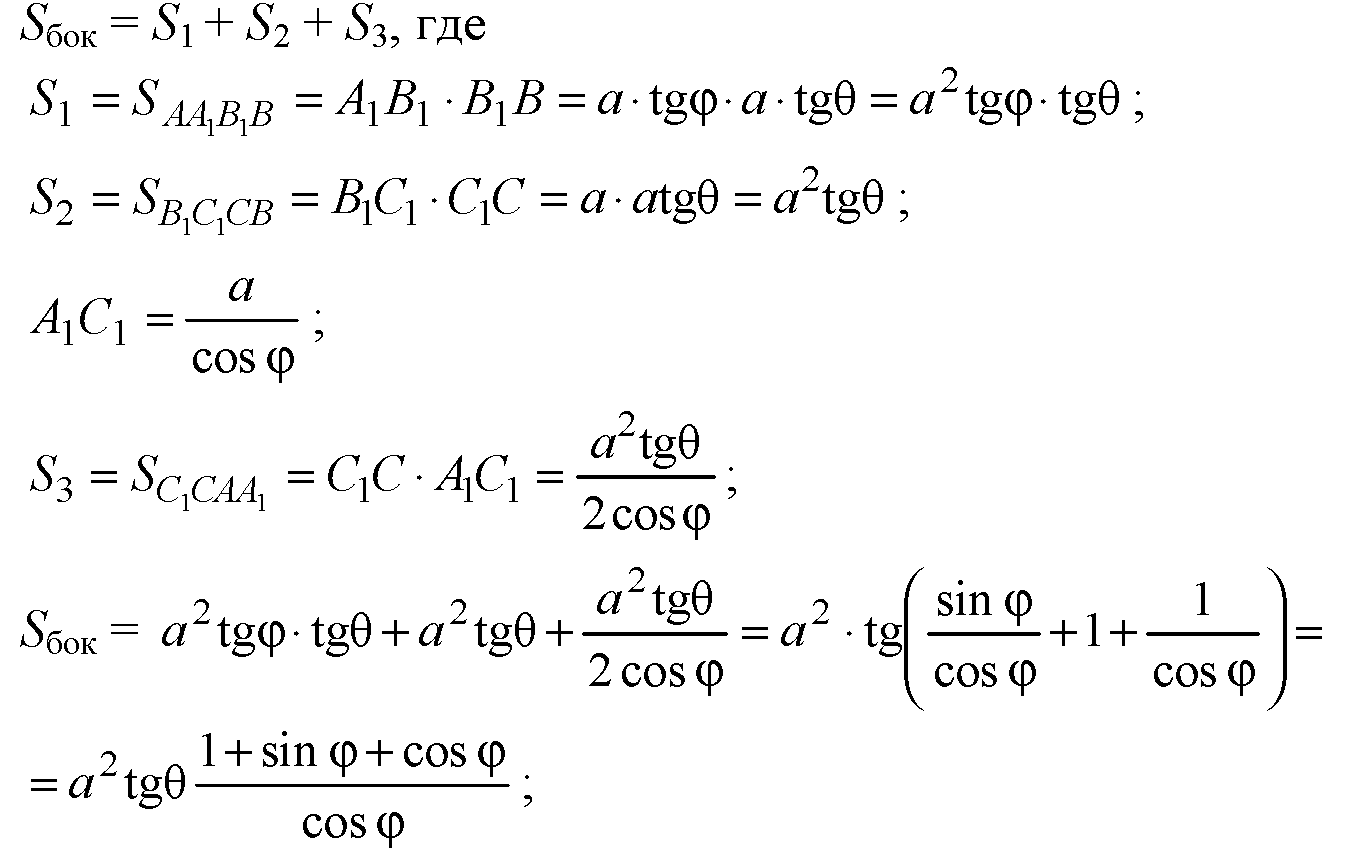
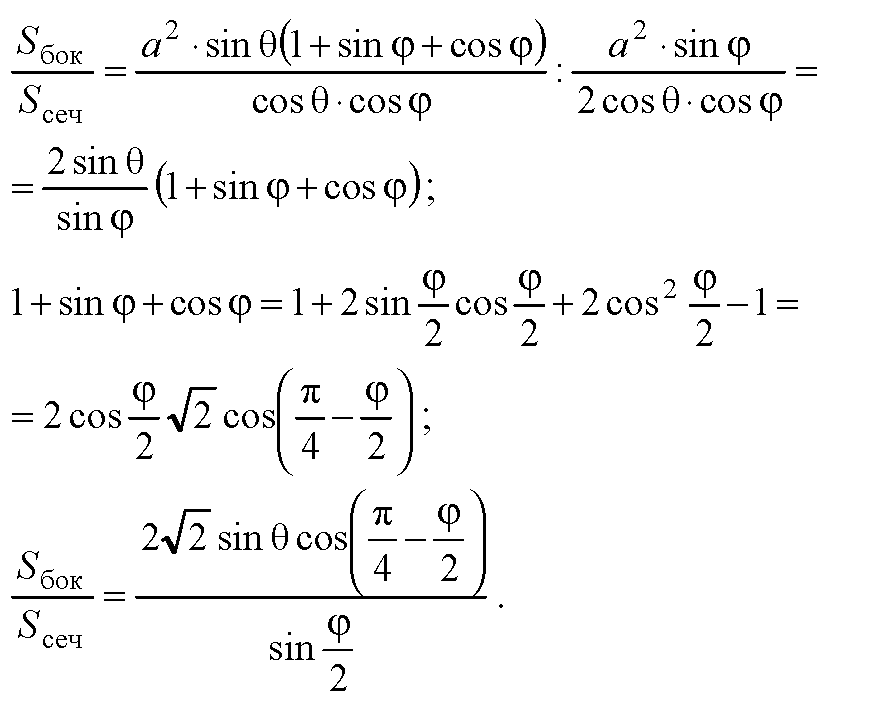
Ответ: