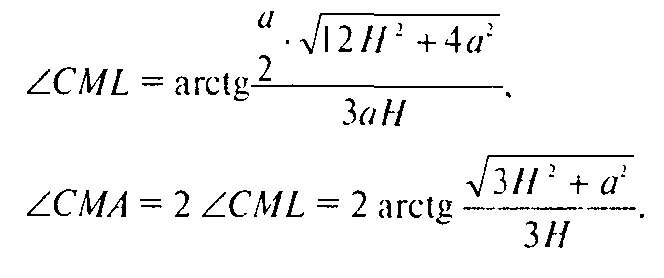Глава III Многогранники. § 2. Пирамида → номер 254 254. В правильной Треугольной пирамиде сторона основания равна а, высота равна Н. Найдите: а) боковое ребро пирамиды; б) плоский угол при вершине пирамиды; в) угол между боковым ребром и плоскостью основания пирамиды; г) угол между боковой гранью и основанием пирамиды; д) двугранный угол при боковом ребре пирамиды.
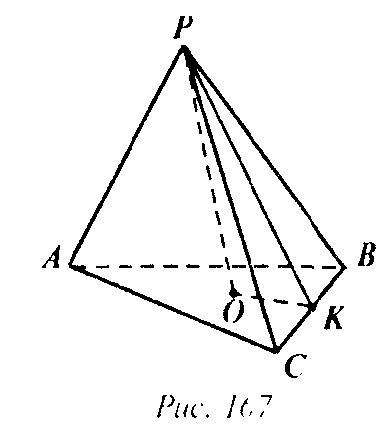
а) PO — высота пирамиды PABC. Радиус R описанной вокруг правильного треугольника окружности равен
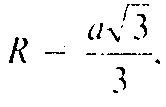
Поэтому
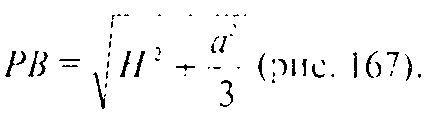
Б)
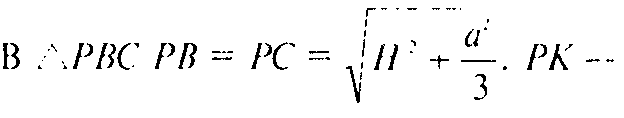
Высота, а следовательно, и медиана. Поэтому
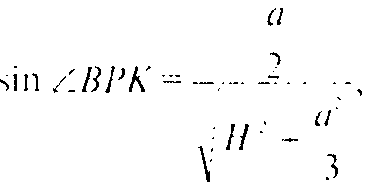
Следовательно
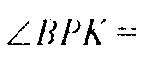
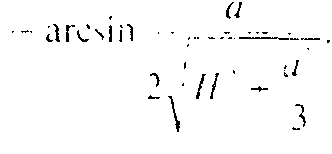
Значит,
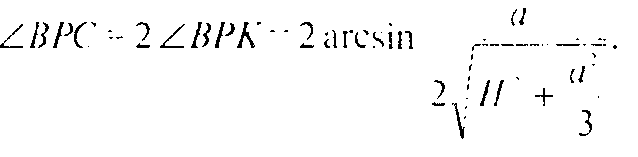
В) Искомый угол — это ∠PBO.
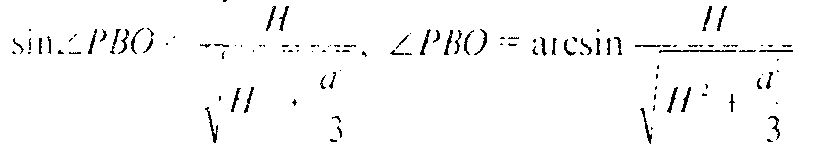
Г) Искомый угол — это угол ∠РКО, так как РК⊥СВ по построению, а ОК⊥ВС по теореме о трех перпендикулярах.
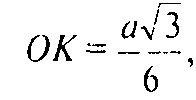
Поэтому
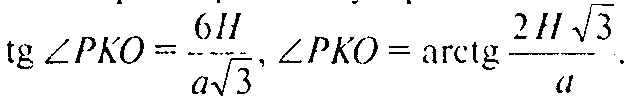
Д) Проведем высоту СМ в ΔРВС (рис. 168). Тогда из равенства ΔPAB и ΔPBC следует, что AM — высота ΔPAB и АМ= СМ. Найдем СМ: пусть ВМ = х, тогда
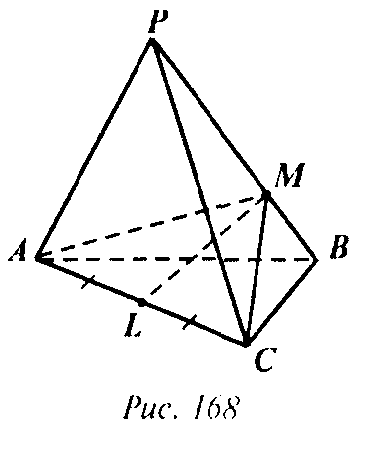
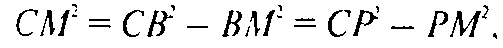
Таким образом
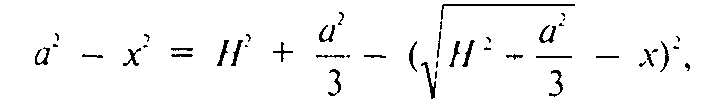
Откуда
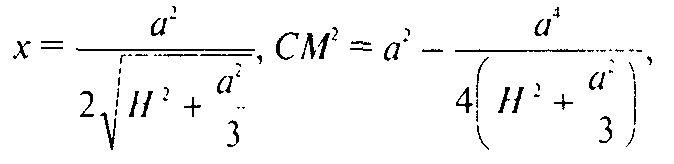
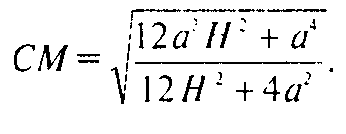
Тогда
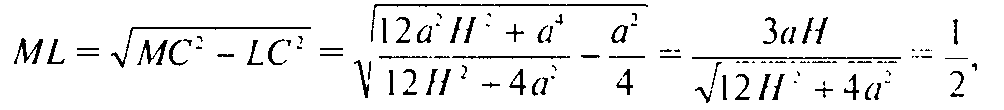
Где ML — высота и медиана ΔАМС. Тогда