Глава III Многогранники. § 3. Правильные многогранники → номер 281 281. В кубе ABCDA1B1C1D1 из вершины D1 проведены диагонали граней D1A, D1C и D1B1 и концы их соединены отрезками, Докажите, что многогранник D1AB1C—правильный тетраэдр. Найдите отношение площадей поверхностей куба и тетраэдра.
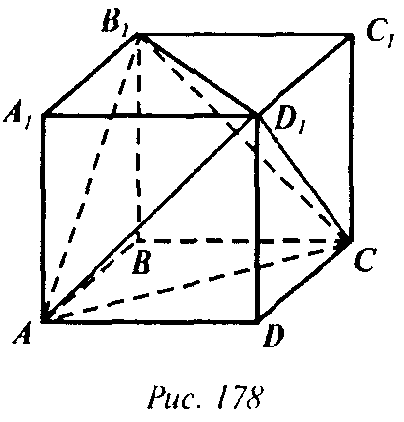
Ребра тетраэдра DAB1С являются диагоналями граней куба. поэтому все ребра тетраэдра равны между собой, но это означает, что все грани тетраэдра равны между собой. Таким образом тетраэдр правильный (рис. 178).
Пусть ребро куба равно а. Тогда
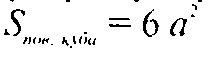
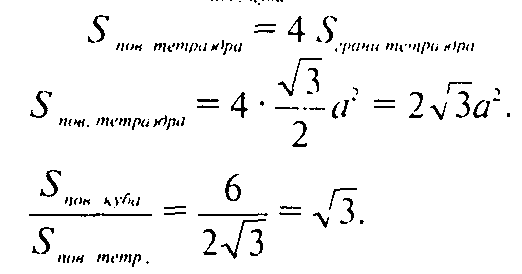
Ответ: √3.
