505*. Медианой тетраэдра называется отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани. Докажите, что медианы тетраэдра пересекаются в одной точке, которая делит каждую медиану в отношении 3:1, считая от вершины

Дополнительные задачи к главе V Метод координат в пространстве → номер 505

Пусть Е1, Е2, E3, E4 — середины ребер ВС, AD, АВ и DC. Точка О — середина отрезка E1Е2; Е2Е3 — средняя линия грани ABD.

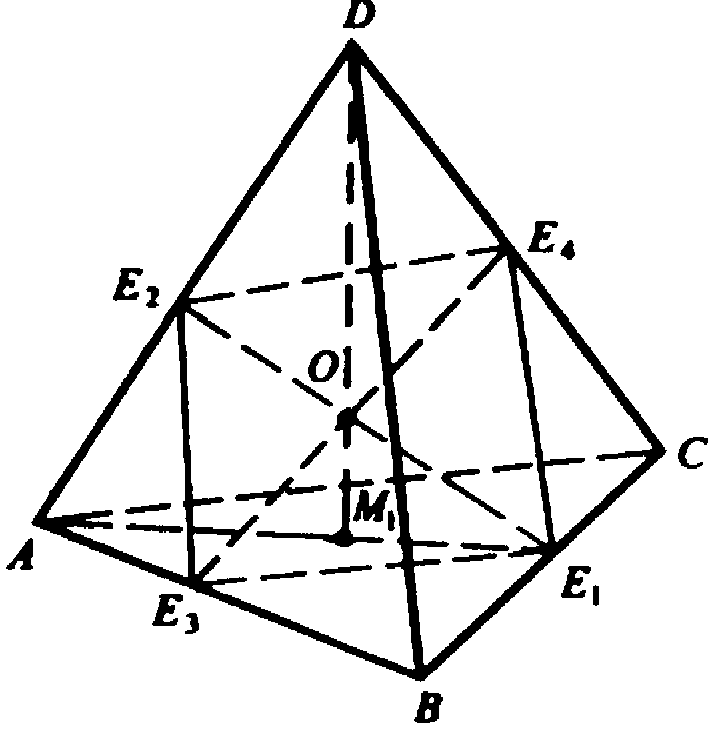
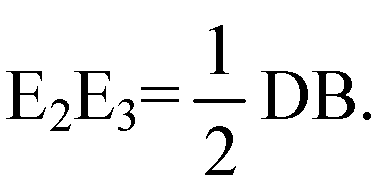
Аналогично

Тогда

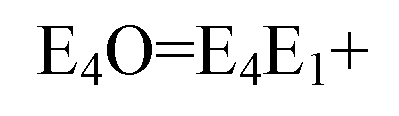
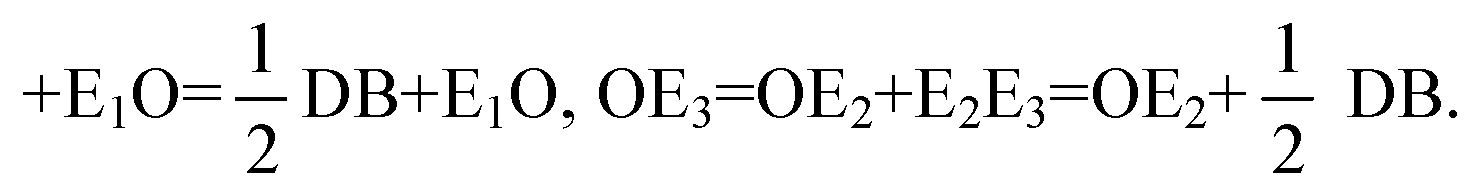
По условию OЕ2=E1O, тогда Е4O=OE3, таким образом О — середина отрезка E3E4.

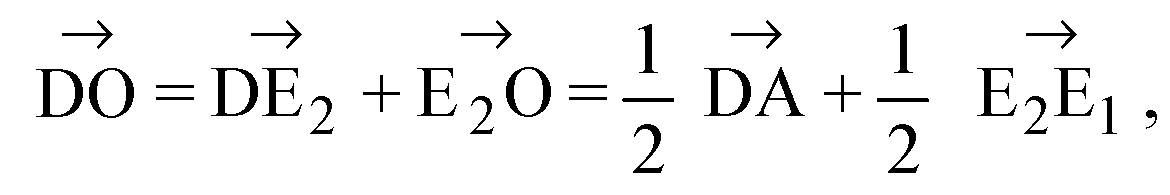
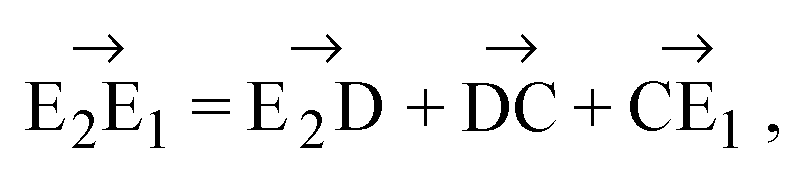
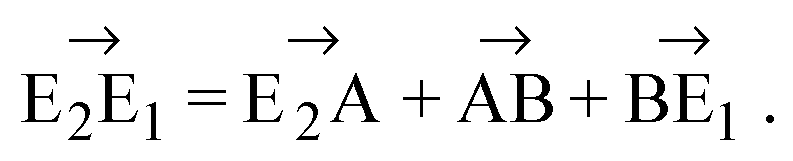
Сложим эти два равенства. Получим:

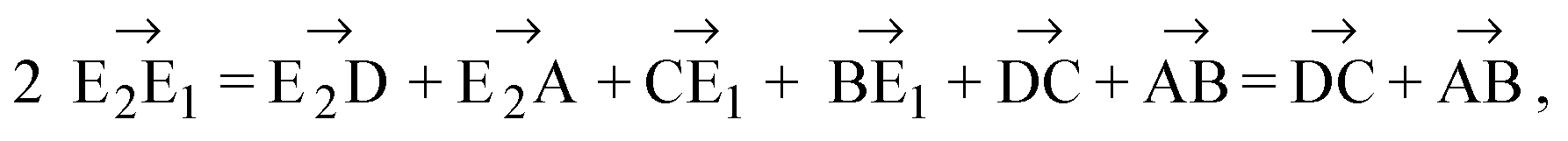
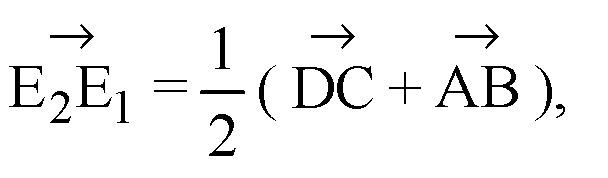
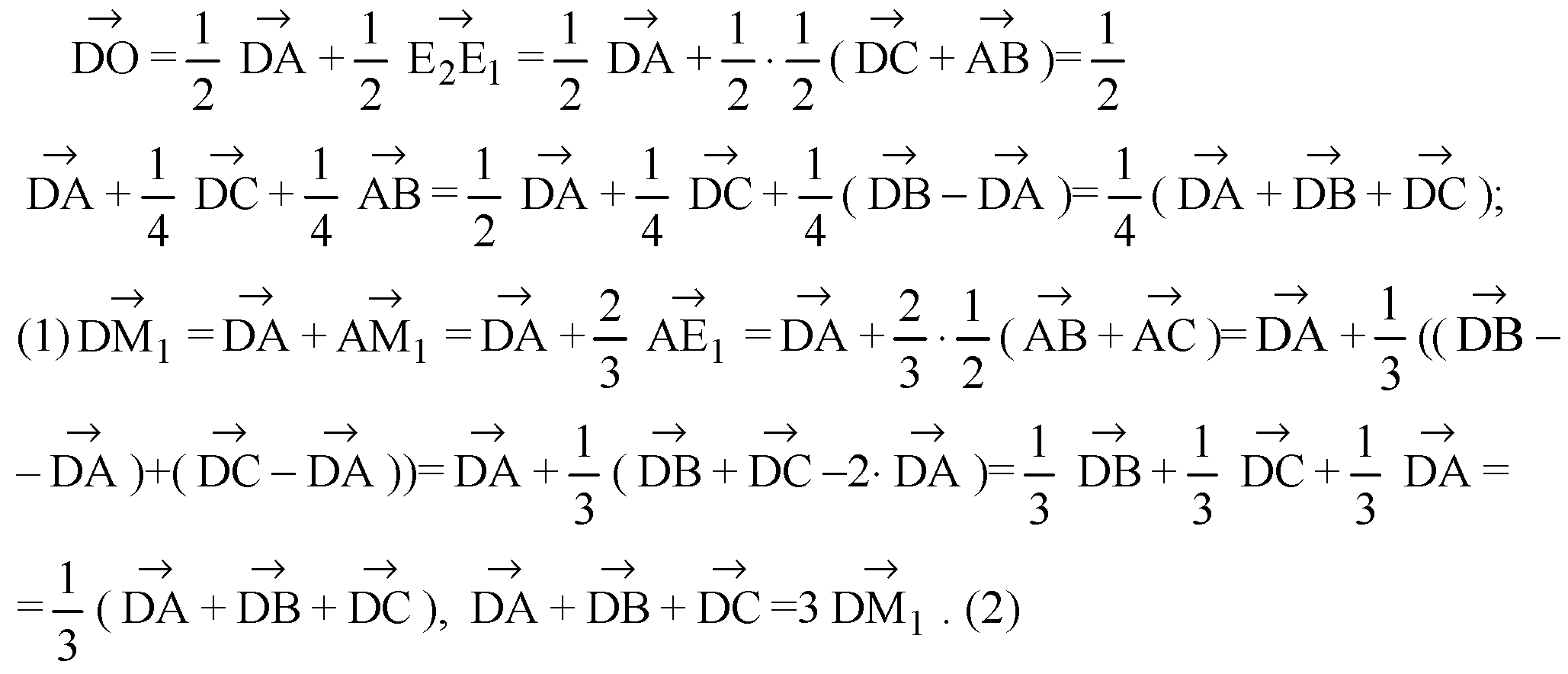
Подставим (2) в (I):

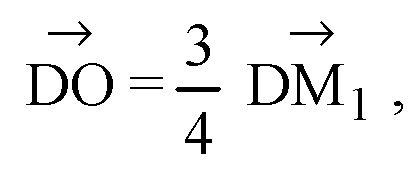
Значит,

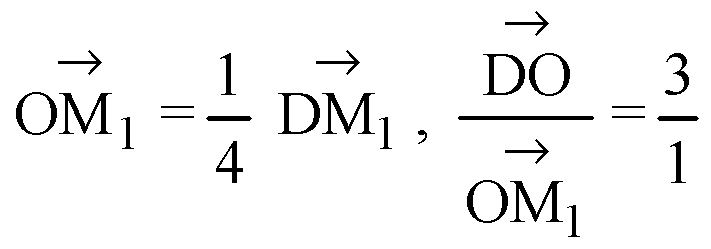
Таким образом, точка О ∈ DM1 и делит DM1 в отношении 3:1, считая от вершины. Аналогично для других медиан.