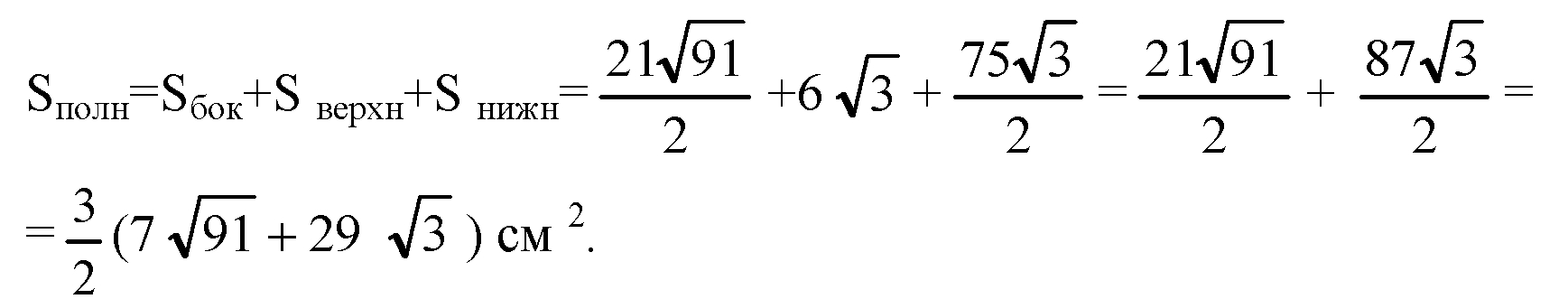Разные задачи на многогранник, цилиндр, конус и шар → номер 631 631. В усеченный конус вписана правильная усеченная n-угольная пирамида (т. е. основания пирамиды вписаны в основания усеченного конуса). Радиусы оснований усеченного конуса равны 2 см и 5 см, а высота равна 4 см. Вычислите площадь полной поверхности пирамиды при: а) n = 3; б) n = 4; в) n= 6.
а) r=2 см, h=4 см, R=5 см.
Обозначим АС=ВС=АВ=а, тогда
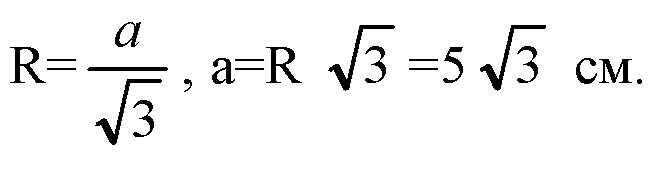
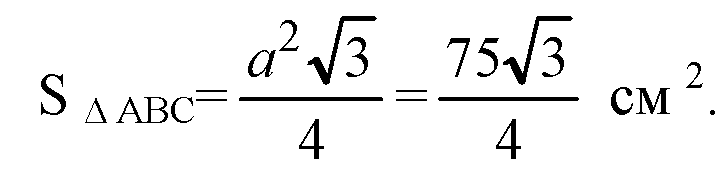
Обозначим
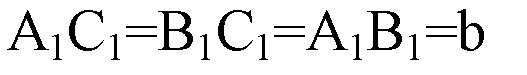
Тогда
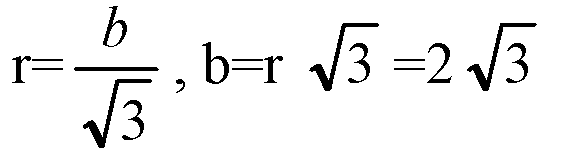
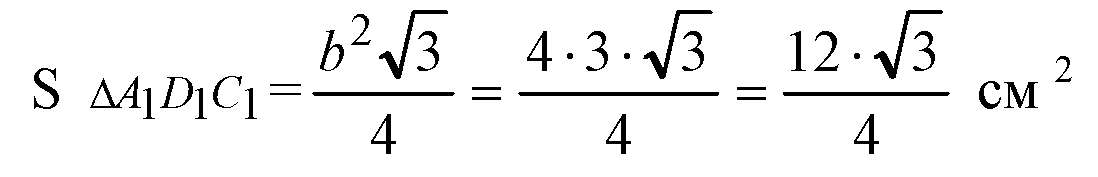
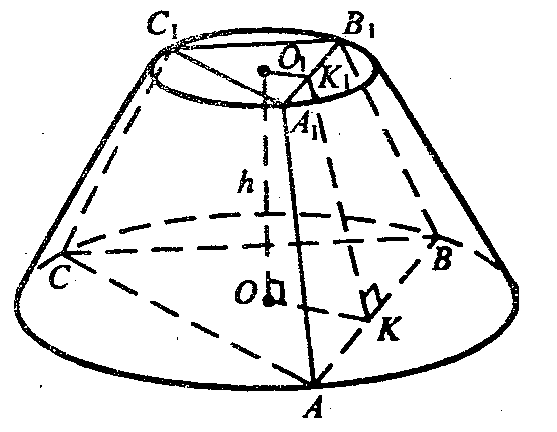
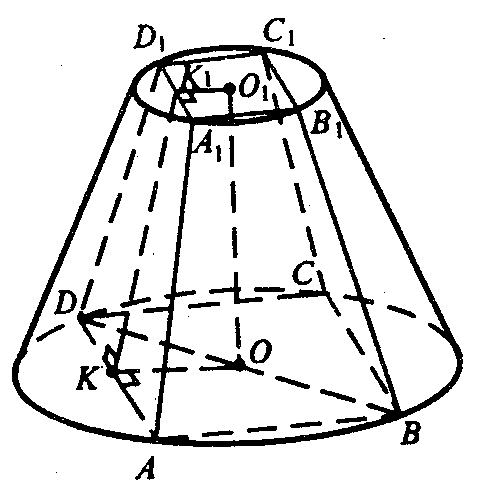
Боковые грани — равные равнобедренные трапеции. Построим ОК1 ⊥ A1B1, ОК ⊥ АВ, отрезок K1K. По теореме о трех перпендикулярах К1K ⊥ АВ.
ОК, О1К1 — радиусы вписанных окружностей в ΔABC и ΔA1B1C1 соответственно.
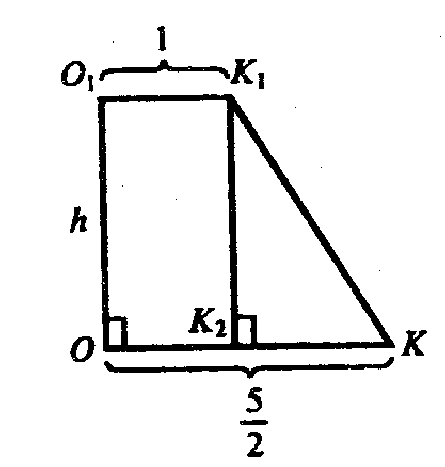
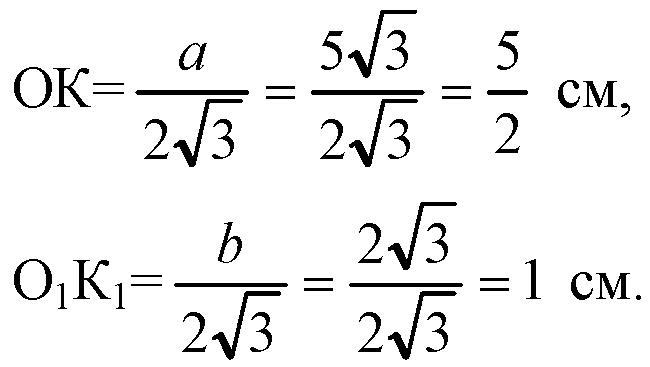
Проведем
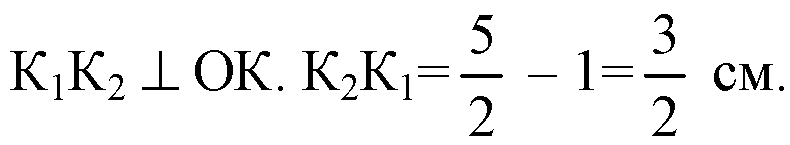
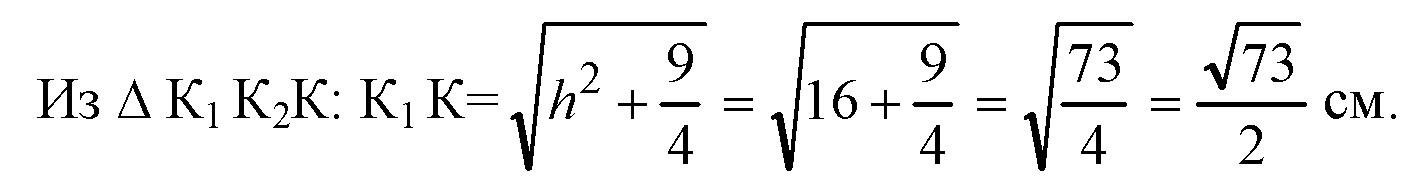
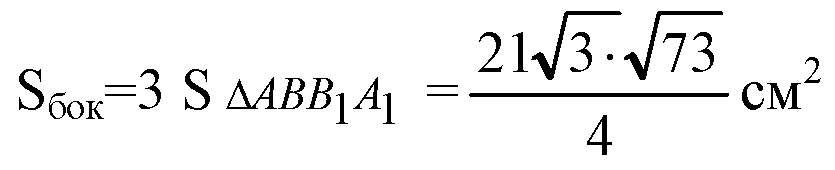
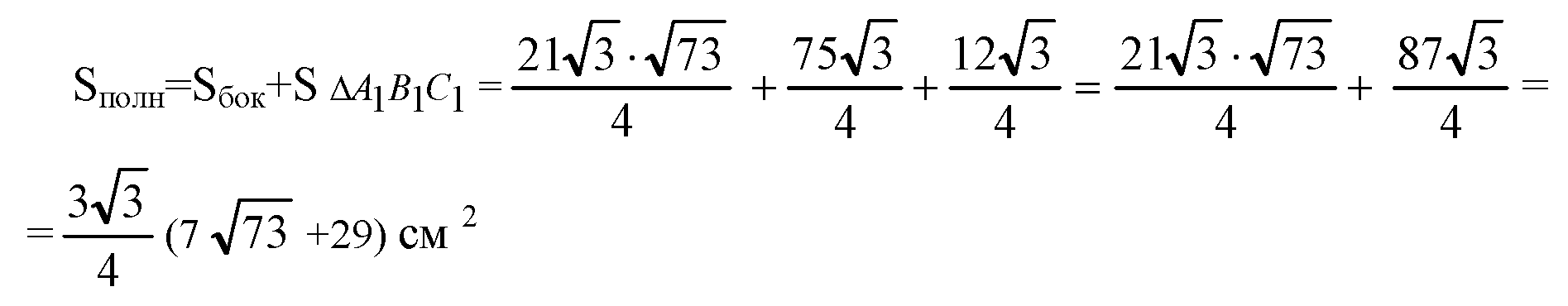
Б) Пусть АВ=а, тогда
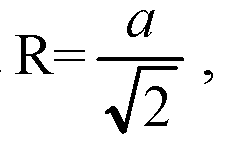
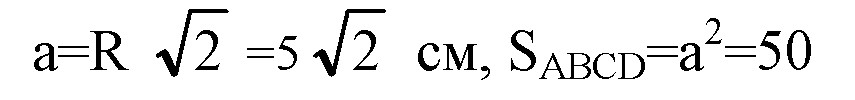
Обозначим A1B1=b, тогда
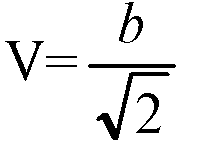
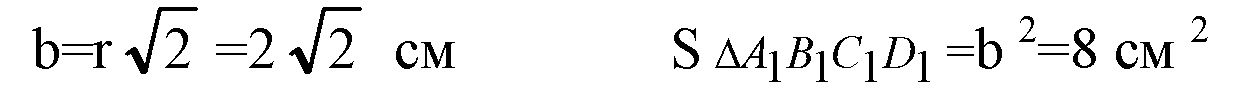
Боковые грани — равные равнобедренные трапеции. Построим О1К1 ⊥ D1A1, OK ⊥ DA, отрезок К1К. По теореме о трех перпендикулярах К1К ⊥ AD.
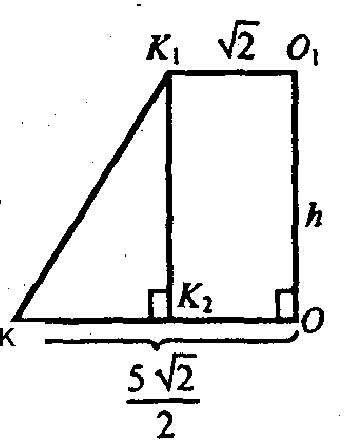
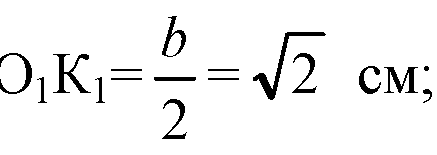
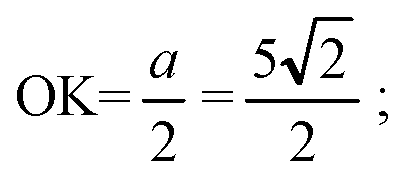
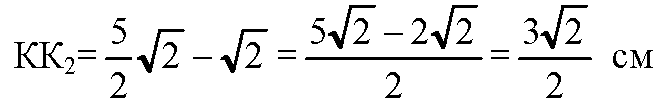
Из ΔK1К2К:
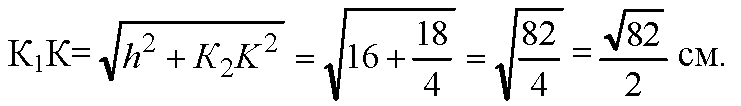
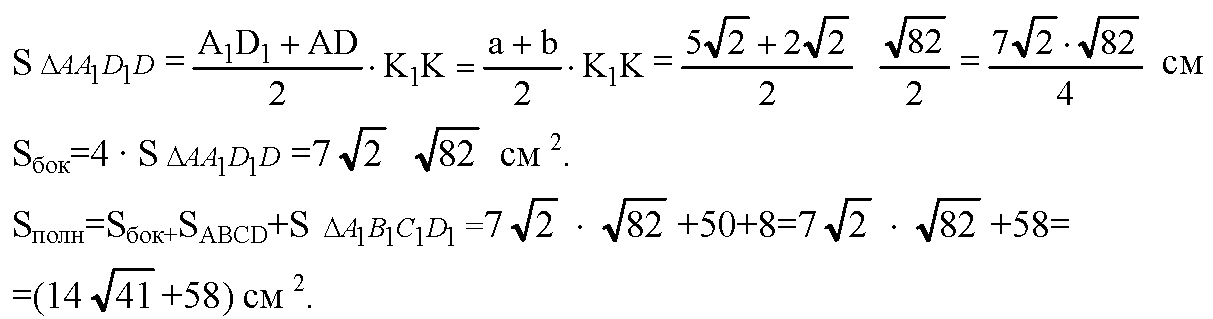
В) Обозначим сторону верхнего основания b, нижнего основания а, а > b; радиус верхнего основания — r, нижнего основания — R. Следовательно, b=r, a=R.
Правильный 6-угольник состоит из 6 равносторонних треугольников; высота которых равна радиусу вписанной в 6-угольник окружности равного х, а в нижний 6-угольник — y. Из планиметрии известно, что:
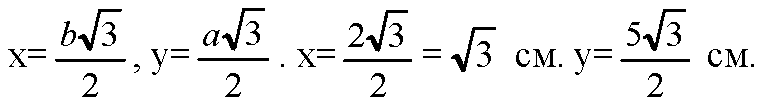
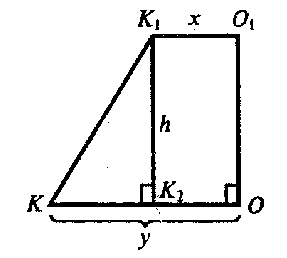
Площадь нижнего основания пирамиды равна
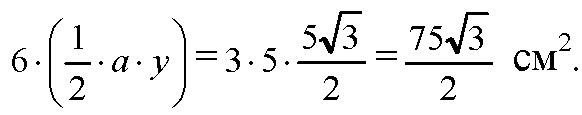
Площадь верхнего основания пирамиды равна
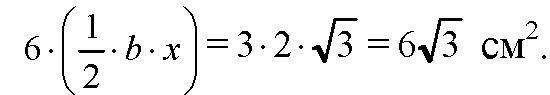
Все 6 боковых граней являются равными равнобедренными трапециями. Вычислим высоту трапеции. В плоскости верхнего основания построим отрезок О1К1 перпендикулярно к стороне 6-угольника; в нижней плоскости построим ОК перпендикулярно одноименной стороне 6-угольника; проведем отрезок К1К.
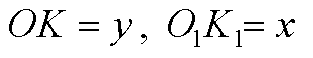
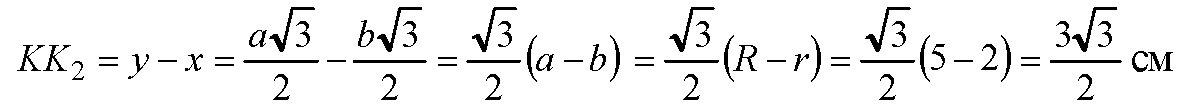
Из ΔK1K2K :
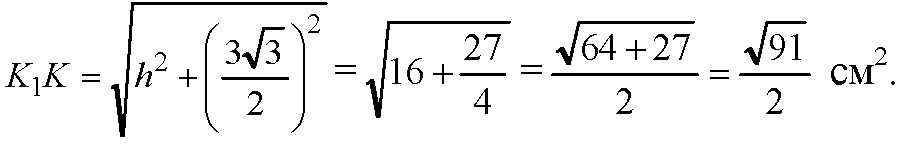
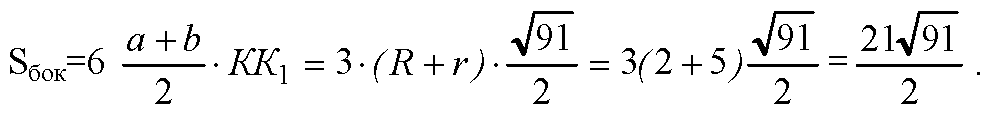
Площадь полной поверхности: