Разные задачи на многогранник, цилиндр, конус и шар → номер 633
Рассмотрим для простоты треугольную правильную пирамиду. SD — высота пирамиды. Построим AE⊥BC, отрезок SE. По теореме о трех перпендикулярах SE⊥CB.
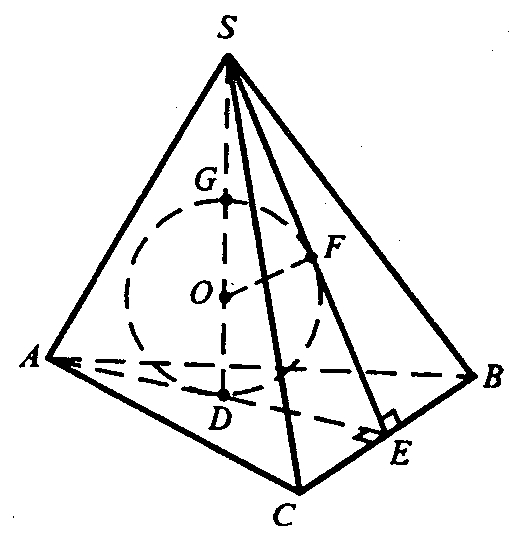
Впишем в ΔSDE полуокружность DFG. Центр О окружности лежит на катете SD, и касается сторон DE и SE. ΔSED вместе с полуокружностью DFG повернем вокруг SD. Тогда точка E опишет окружность, вписанную в ΔABC, то есть гипотенуза SE при вращении останется внутри пирамиды, кроме трех положений, когда SE совпадает с высотой боковых граней.
Т. е. сфера, образованная вращением полуокружности DFG, имеет единственную общую точку с каждой из боковых граней. Эта сфера касается основания пирамиды в точке D.
Центр вписанной в пирамиду ΔABC сферы лежит на высоте SD.
