64. Три прямые, проходящие через одну точку и не лежащие в одной плоскости, пересекают одну из параллельных плоскостей в точках A1, B1 и C1 а другую — в точках A2, B2 и C2. Докажите, что треугольники A1B1C1 и А2В2С2 подобны

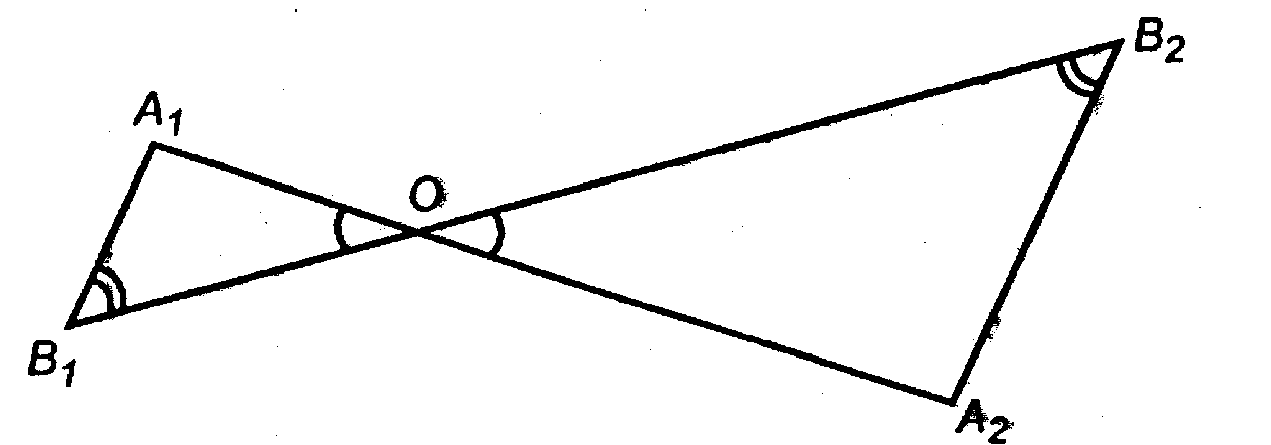
Глава I Параллельность прямых и плоскостей. §3 Параллельность плоскостей → номер 64 64. Три прямые, проходящие через одну точку и не лежащие в одной плоскости, пересекают одну из параллельных плоскостей в точках A1, B1 и C1 а другую — в точках A2, B2 и C2. Докажите, что треугольники A1B1C1 и А2В2С2 подобны.

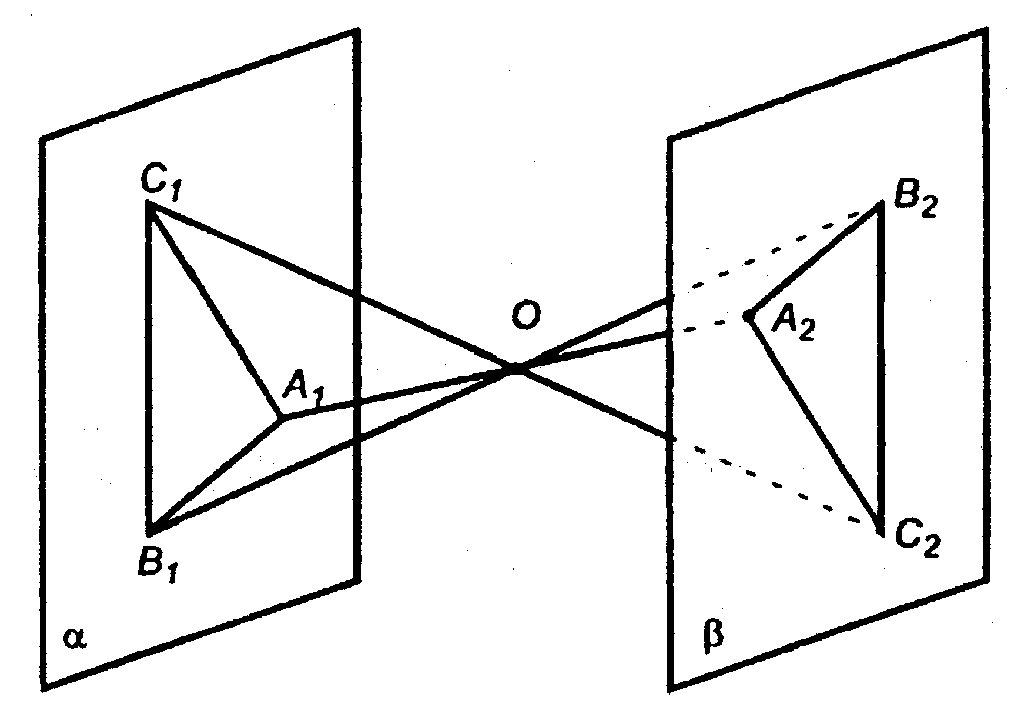
Две пересекающиеся прямые единственным образом задают плоскость.

Прямые А1А2 и В1В2 пересекаются и задают плоскость А1В1В2.

По свойству параллельных

Плоскостей (п. 11, 1о)

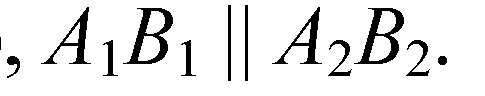
Аналогично:

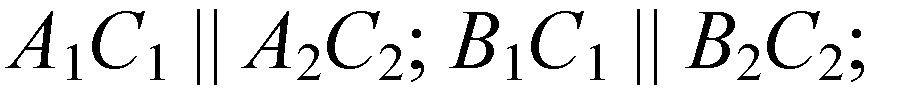
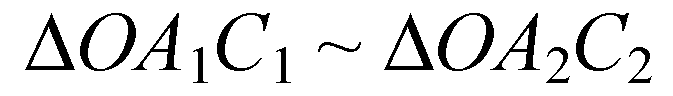
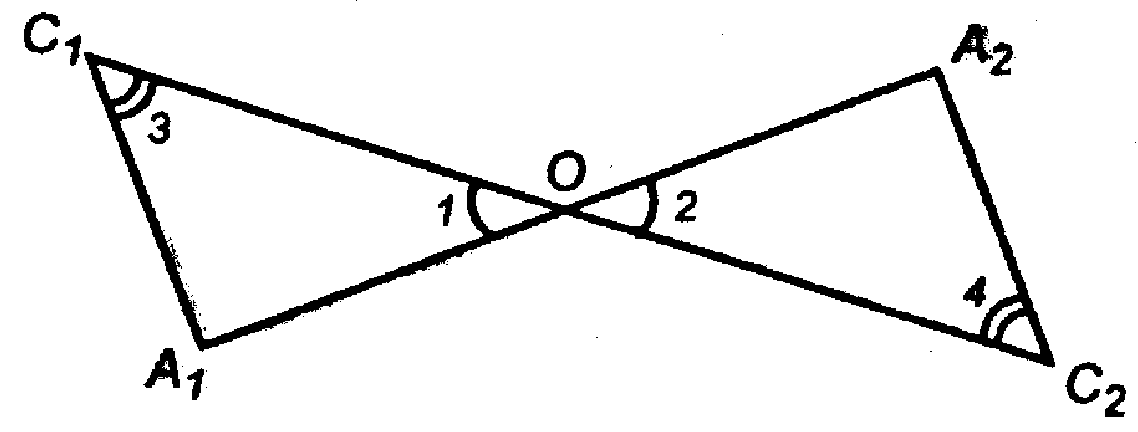
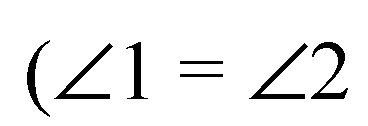
— как вертикальные,

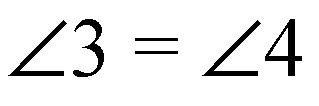
Как накрест лежащие);

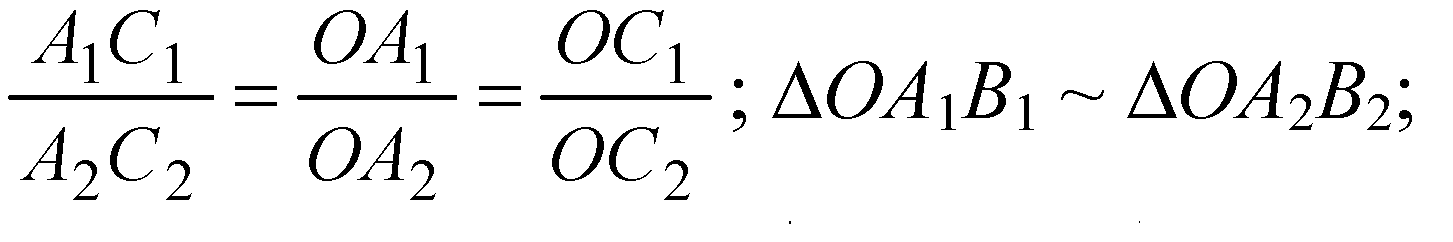
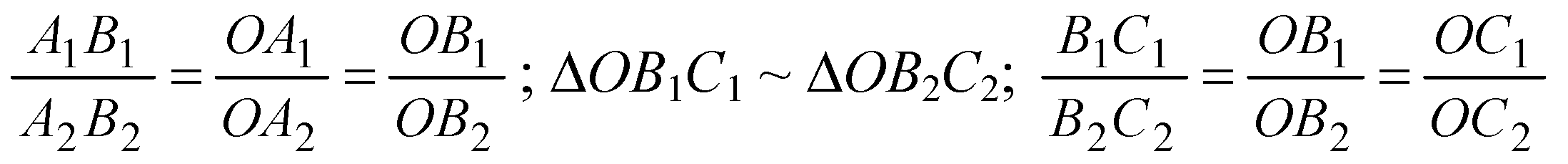
Учитывая полученные соотношения, получим

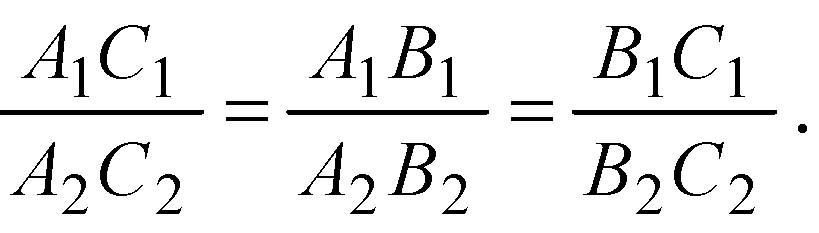
Значит,

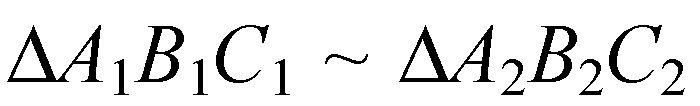
По третьему признаку подобия (пропорциональность сторон).