Задачи повышенной трудности → номер 768
Пусть плоскость а, проходящая через A перпендикулярно ВС, пересекает ВС в точке D(рис. 569); произвольная плоскость μ, проходящая через ВС, пересекает α по прямой m, ω — окружность без точки А с диаметром AD, лежащая в плоскости α, M∈m∩ω.
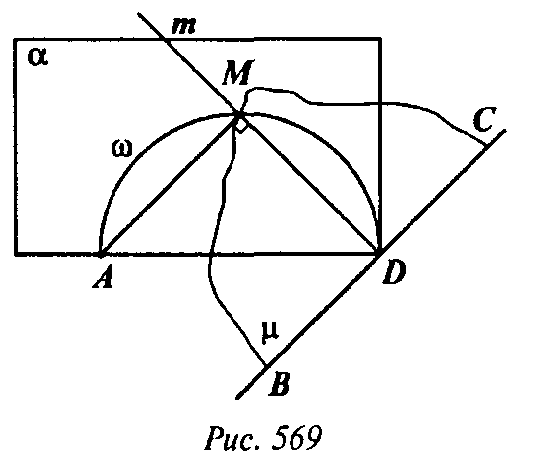
Так как AM∩α, то AM⊥BC a так как M ∈ ω, то AM ⊥ μ, так как ∠AMD = 90°, как опирающийся на диаметр. Если М не лежит на ω, то она не принадлежит искомому множеству (иначе нарушаются теоремы о единственности пер-пендикуляра, опущенного из данной точки на данную прямую или плоскость. Таким образом, ω — искомое множество точек.
