Глава I Параллельность прямых и плоскостей. §4 Тетраэдр и параллелепипед. → номер 78 78. На рисунке 42 изображен параллелепипед ABCDA1B1C1D1, на ребрах которого отмечены точки М, N, М1 и N1 так, что AM = CN=A1M1 = C1N1. Докажите, что MBNDM1B1N1D1 — параллелепипед.
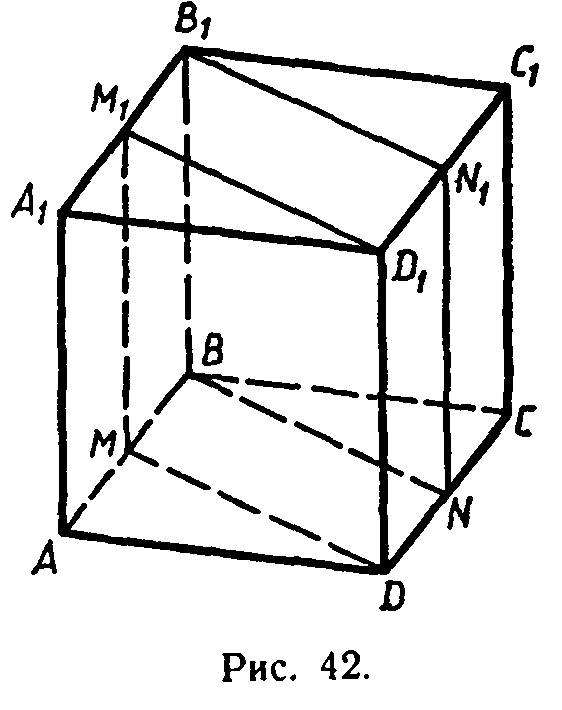
ABCD — параллелограмм по условию,
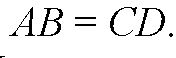
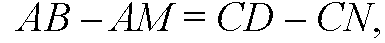
То есть
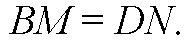
Но
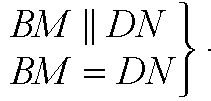
→ по признаку параллелограмма,
MBND — параллелограмм.
Аналогично получим, что N1B1M1D1 — параллелограмм.
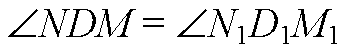
— как углы с соответственно параллельными и
Одинаково направленными сторонами.
Параллелограммы MBND и M1B1N1D1 равны, так как равны их
Соответствующие стороны
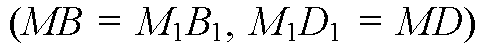
И угол между ними (п. 5).
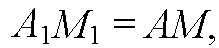
Поэтому
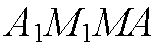
— параллелограмм,
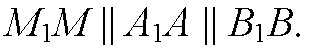
Аналогично,
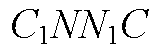
— параллелограмм,
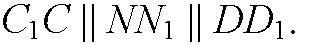
Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны, поэтому
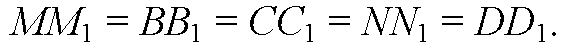
По признаку параллелограмма 4-угольники МВВ1М1, BNN1B1, DNN1 D1 и MDD1 M1 — параллелограммы.
По определению (п. 13) MBNDM1B1N1D1 — параллелепипед.
