Глава I Параллельность прямых и плоскостей. §4 Тетраэдр и параллелепипед. → номер 79
А) Сечение плоскостью АВС1.
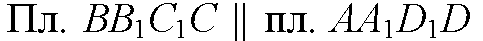
По свойству параллелепипеда, отсюда
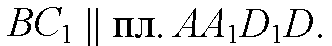
Точка А общая для плоскостей АВС1 и AA1D1D — плоскости пересекаются по прямой, проходящей через т. А и параллельной ВС1 (п. 11.1о), очевидно, это AD.
Искомое сечение — четырехугольник ABC1D1.
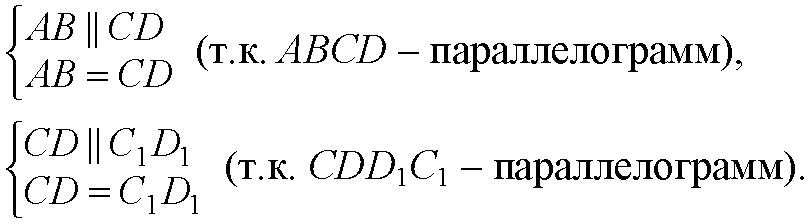
Отсюда
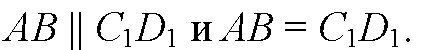
Значит, ABC1D1 — параллелограмм, т. к. его противоположные стороны параллельны и равны.
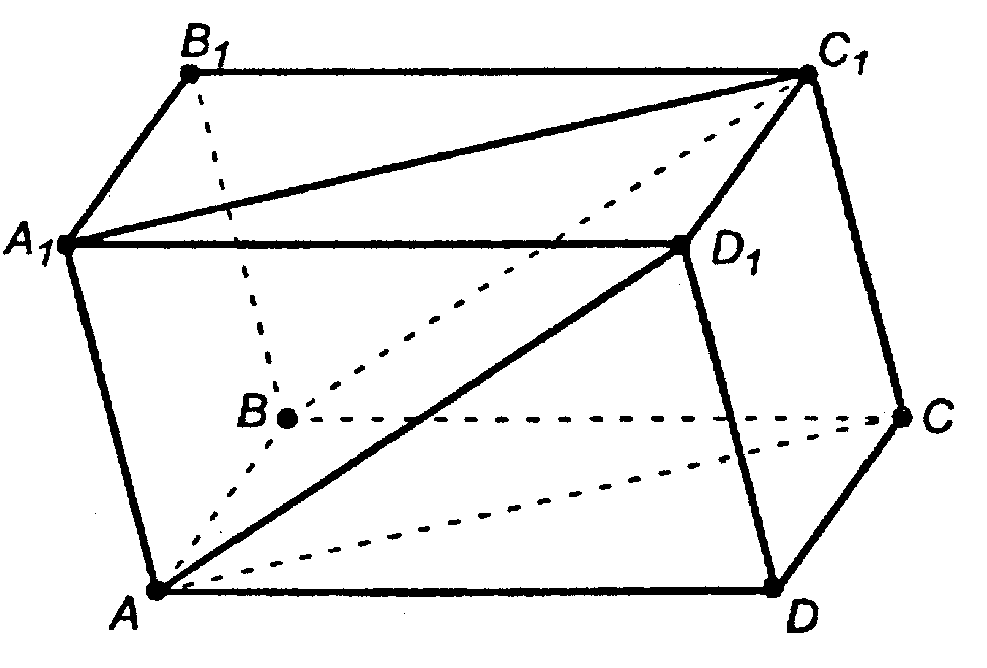
Б) Сечение плоскостью АСС1.
Плоскости граней В1С1СВ и A1D1DA пересечены плоскостью А1С1СА, линии пересечения параллельны, АА1 || CC1.
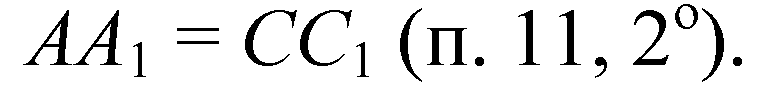
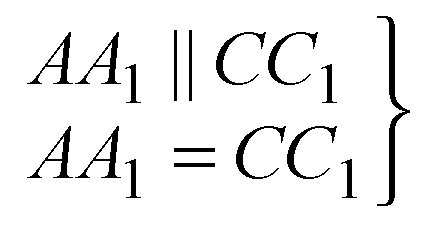
По признаку параллелограмма, АА1С1С — параллело
Грамм.
